Menu Close

Question-173668

Tinku Tara 0 Comments
Pin




Question Number 173668 by mr W last updated on 16/Jul/22
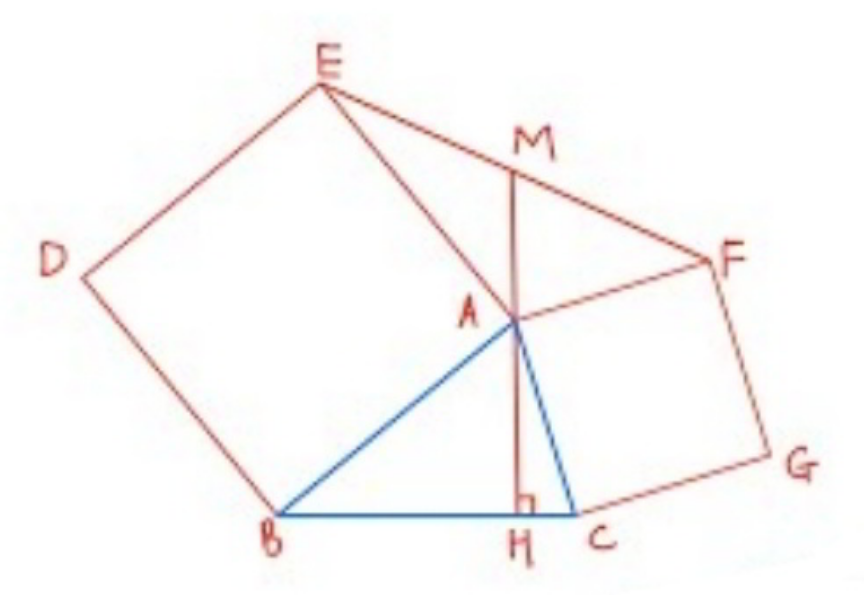
Commented by mr W last updated on 16/Jul/22
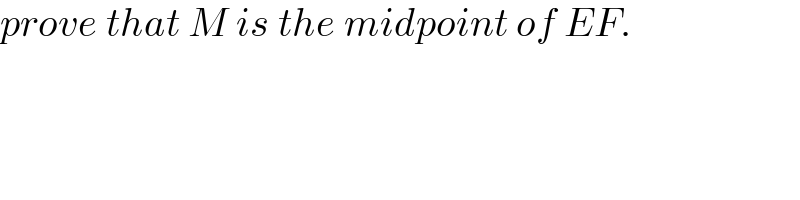
prove that M is the midpoint of EF.
$${prove}\:{that}\:{M}\:{is}\:{the}\:{midpoint}\:{of}\:{EF}. \\ $$
Answered by mr W last updated on 16/Jul/22
Answered by mr W last updated on 16/Jul/22
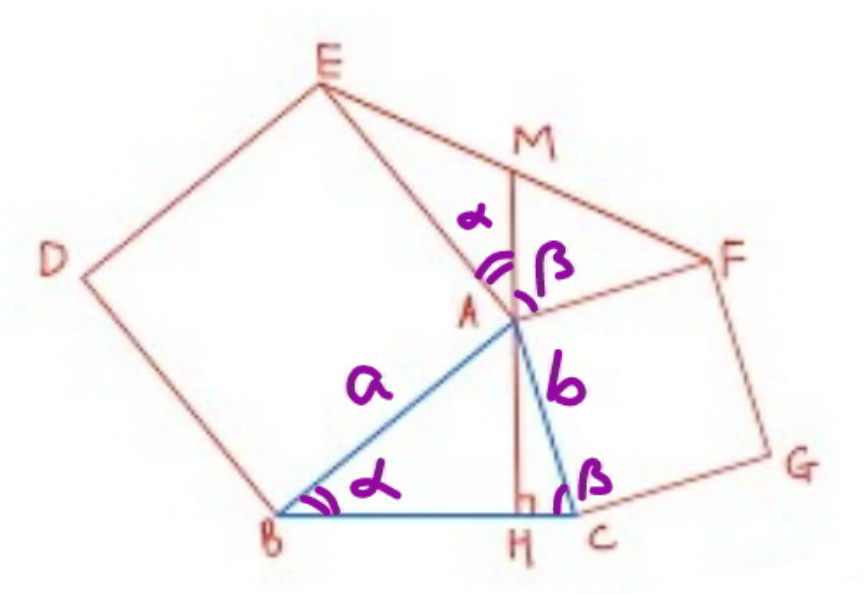
Commented by infinityaction last updated on 16/Jul/22
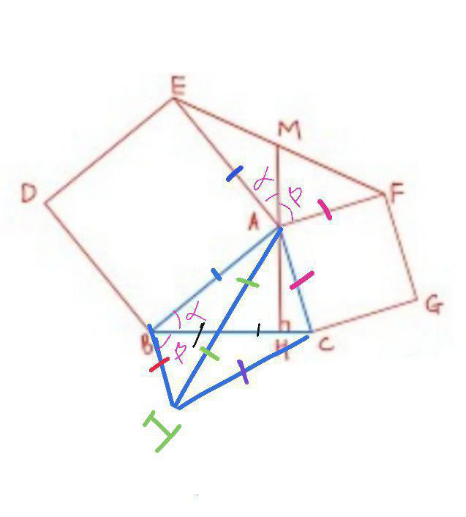
Commented by infinityaction last updated on 16/Jul/22
ABI⋍AEF
$${ABI}\backsimeq{AEF} \\ $$
Commented by Tawa11 last updated on 16/Jul/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mindispower last updated on 16/Jul/22
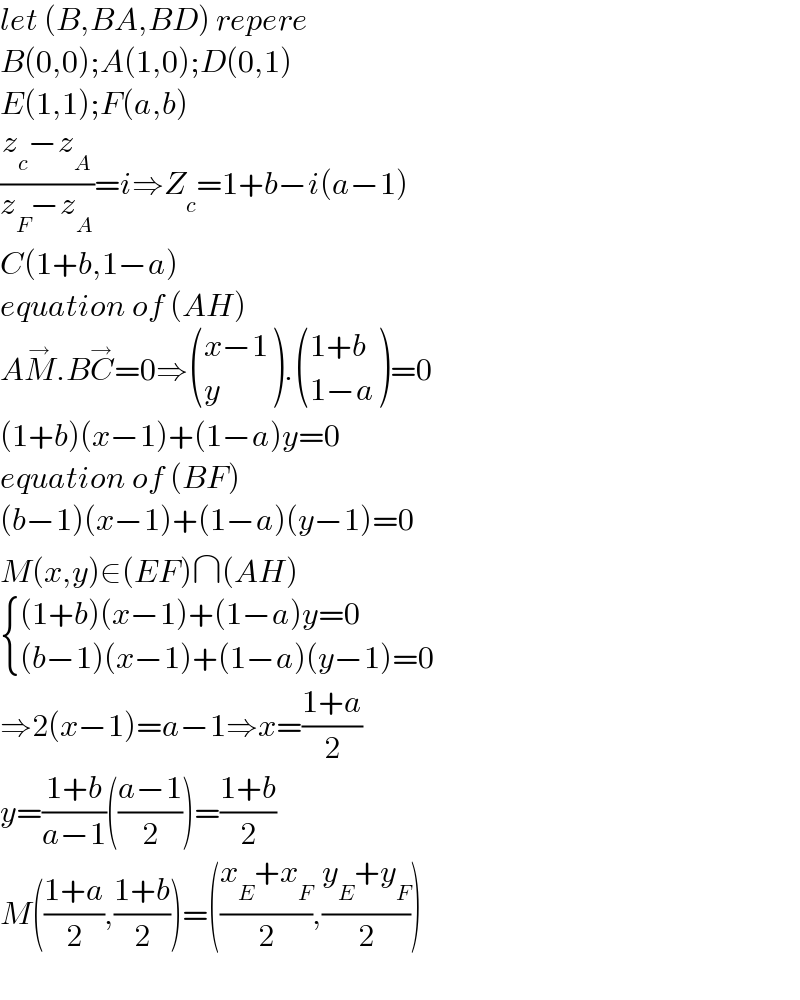
let (B,BA,BD) repere B(0,0);A(1,0);D(0,1) E(1,1);F(a,b) ((z_c −z_A )/(z_F −z_A ))=i⇒Z_c =1+b−i(a−1) C(1+b,1−a) equation of (AH) AM^→ .BC^→ =0⇒ (((x−1)),(y) ). (((1+b)),((1−a)) )=0 (1+b)(x−1)+(1−a)y=0 equation of (BF) (b−1)(x−1)+(1−a)(y−1)=0 M(x,y)∈(EF)∩(AH) { (((1+b)(x−1)+(1−a)y=0)),(((b−1)(x−1)+(1−a)(y−1)=0)) :} ⇒2(x−1)=a−1⇒x=((1+a)/2) y=((1+b)/(a−1))(((a−1)/2))=((1+b)/2) M(((1+a)/2),((1+b)/2))=(((x_E +x_F )/2),((y_E +y_F )/2))
$${let}\:\left({B},{BA},{BD}\right)\:{repere}\: \\ $$$${B}\left(\mathrm{0},\mathrm{0}\right);{A}\left(\mathrm{1},\mathrm{0}\right);{D}\left(\mathrm{0},\mathrm{1}\right) \\ $$$${E}\left(\mathrm{1},\mathrm{1}\right);{F}\left({a},{b}\right) \\ $$$$\frac{{z}_{{c}} −{z}_{{A}} }{{z}_{{F}} −{z}_{{A}} }={i}\Rightarrow{Z}_{{c}} =\mathrm{1}+{b}−{i}\left({a}−\mathrm{1}\right) \\ $$$${C}\left(\mathrm{1}+{b},\mathrm{1}−{a}\right) \\ $$$${equation}\:{of}\:\left({AH}\right) \\ $$$${A}\overset{\rightarrow} {{M}}.{B}\overset{\rightarrow} {{C}}=\mathrm{0}\Rightarrow\begin{pmatrix}{{x}−\mathrm{1}}\\{{y}}\end{pmatrix}.\begin{pmatrix}{\mathrm{1}+{b}}\\{\mathrm{1}−{a}}\end{pmatrix}=\mathrm{0} \\ $$$$\left(\mathrm{1}+{b}\right)\left({x}−\mathrm{1}\right)+\left(\mathrm{1}−{a}\right){y}=\mathrm{0} \\ $$$${equation}\:{of}\:\left({BF}\right) \\ $$$$\left({b}−\mathrm{1}\right)\left({x}−\mathrm{1}\right)+\left(\mathrm{1}−{a}\right)\left({y}−\mathrm{1}\right)=\mathrm{0} \\ $$$${M}\left({x},{y}\right)\in\left({EF}\right)\cap\left({AH}\right) \\ $$$$\begin{cases}{\left(\mathrm{1}+{b}\right)\left({x}−\mathrm{1}\right)+\left(\mathrm{1}−{a}\right){y}=\mathrm{0}}\\{\left({b}−\mathrm{1}\right)\left({x}−\mathrm{1}\right)+\left(\mathrm{1}−{a}\right)\left({y}−\mathrm{1}\right)=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\mathrm{2}\left({x}−\mathrm{1}\right)={a}−\mathrm{1}\Rightarrow{x}=\frac{\mathrm{1}+{a}}{\mathrm{2}} \\ $$$${y}=\frac{\mathrm{1}+{b}}{{a}−\mathrm{1}}\left(\frac{{a}−\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{1}+{b}}{\mathrm{2}} \\ $$$${M}\left(\frac{\mathrm{1}+{a}}{\mathrm{2}},\frac{\mathrm{1}+{b}}{\mathrm{2}}\right)=\left(\frac{{x}_{{E}} +{x}_{{F}} }{\mathrm{2}},\frac{{y}_{{E}} +{y}_{{F}} }{\mathrm{2}}\right) \\ $$$$ \\ $$
Commented by Tawa11 last updated on 16/Jul/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by mindispower last updated on 17/Jul/22
withe Pleasur have a nice Day
$${withe}\:{Pleasur}\:{have}\:{a}\:{nice}\:{Day} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *