Question Number 17374 by ajfour last updated on 04/Jul/17
Commented by ajfour last updated on 04/Jul/17

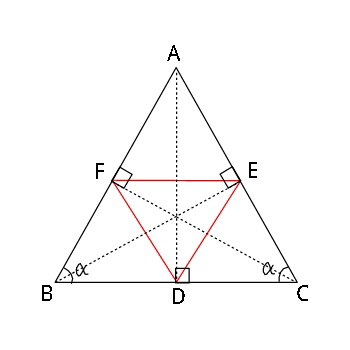
$$\mathrm{The}\:\mathrm{base}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{an}\:\mathrm{isosceles} \\ $$$$\bigtriangleup\mathrm{ABC}\:\mathrm{is}\:\alpha\:\left(>\mathrm{45}°\right),\:\mathrm{the}\:\mathrm{area}\:\mathrm{of} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{S}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{a} \\ $$$$\mathrm{triangle}\:\left(\bigtriangleup\mathrm{DEF}\right)\:\mathrm{whose}\:\mathrm{vertices} \\ $$$$\mathrm{are}\:\mathrm{the}\:\mathrm{feet}\:\mathrm{of}\:\mathrm{the}\:\mathrm{altitudes}\:\mathrm{of}\: \\ $$$$\bigtriangleup\mathrm{ABC}. \\ $$
Answered by b.e.h.i.8.3.4.17@gmail.com last updated on 06/Jul/17
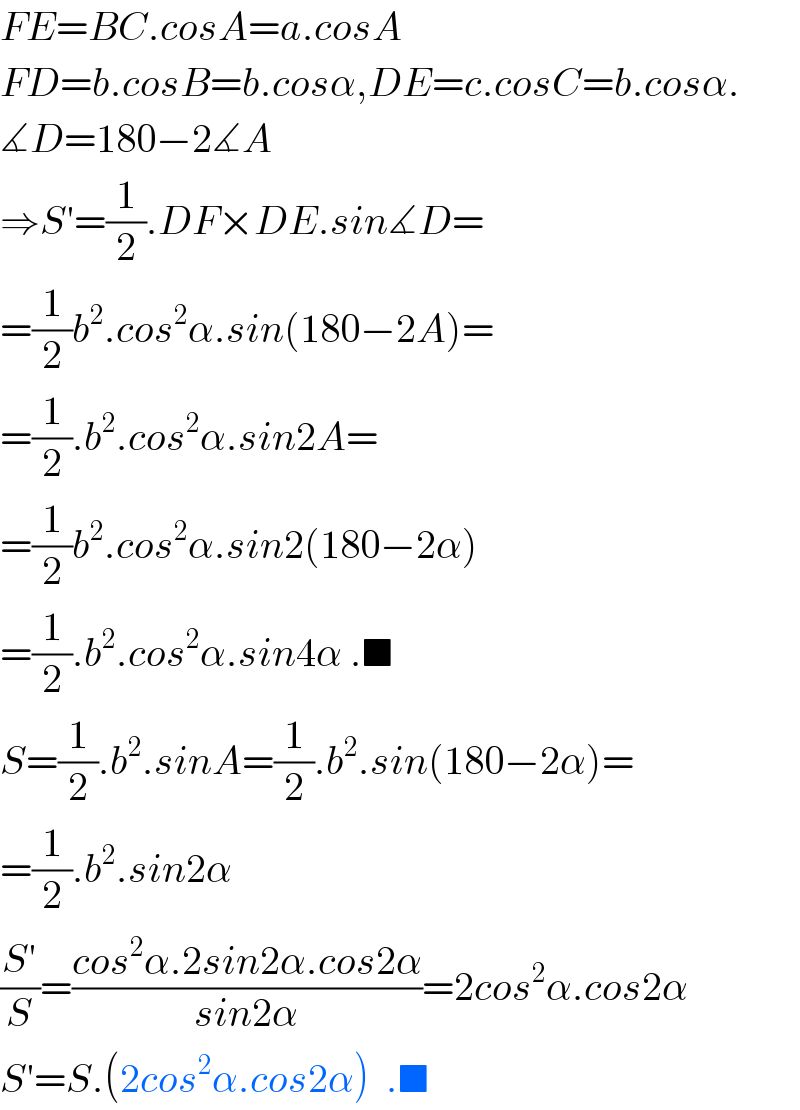
$${FE}={BC}.{cosA}={a}.{cosA} \\ $$$${FD}={b}.{cosB}={b}.{cos}\alpha,{DE}={c}.{cosC}={b}.{cos}\alpha. \\ $$$$\measuredangle{D}=\mathrm{180}−\mathrm{2}\measuredangle{A} \\ $$$$\Rightarrow{S}'=\frac{\mathrm{1}}{\mathrm{2}}.{DF}×{DE}.{sin}\measuredangle{D}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{b}^{\mathrm{2}} .{cos}^{\mathrm{2}} \alpha.{sin}\left(\mathrm{180}−\mathrm{2}{A}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.{b}^{\mathrm{2}} .{cos}^{\mathrm{2}} \alpha.{sin}\mathrm{2}{A}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{b}^{\mathrm{2}} .{cos}^{\mathrm{2}} \alpha.{sin}\mathrm{2}\left(\mathrm{180}−\mathrm{2}\alpha\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.{b}^{\mathrm{2}} .{cos}^{\mathrm{2}} \alpha.{sin}\mathrm{4}\alpha\:.\blacksquare \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}.{b}^{\mathrm{2}} .{sinA}=\frac{\mathrm{1}}{\mathrm{2}}.{b}^{\mathrm{2}} .{sin}\left(\mathrm{180}−\mathrm{2}\alpha\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.{b}^{\mathrm{2}} .{sin}\mathrm{2}\alpha \\ $$$$\frac{{S}'}{{S}}=\frac{{cos}^{\mathrm{2}} \alpha.\mathrm{2}{sin}\mathrm{2}\alpha.{cos}\mathrm{2}\alpha}{{sin}\mathrm{2}\alpha}=\mathrm{2}{cos}^{\mathrm{2}} \alpha.{cos}\mathrm{2}\alpha \\ $$$${S}'={S}.\left(\mathrm{2}{cos}^{\mathrm{2}} \alpha.{cos}\mathrm{2}\alpha\right)\:\:.\blacksquare \\ $$
Commented by ajfour last updated on 08/Jul/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\:\mathrm{S}'=−\mathrm{2Scos}\:\mathrm{2}\alpha\mathrm{cos}\:^{\mathrm{2}} \alpha\:. \\ $$$$\:\mathrm{you}\:\mathrm{dropped}\:\mathrm{the}\:\mathrm{minua}\:\mathrm{sign}\:\mathrm{here} \\ $$$$\:\:\mathrm{sin}\:\mathrm{2}\left(\mathrm{180}−\mathrm{2}\alpha\right)=−\mathrm{sin}\:\mathrm{4}\alpha\:. \\ $$
