Question-173776

Question Number 173776 by AgniMath last updated on 18/Jul/22

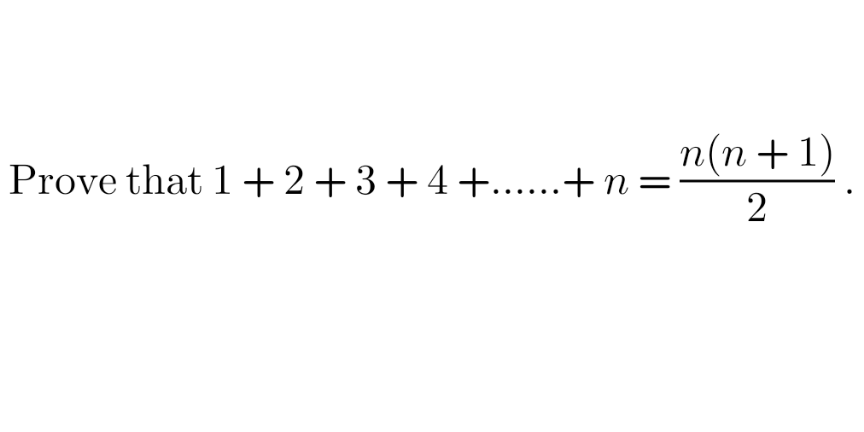
Answered by thfchristopher last updated on 18/Jul/22

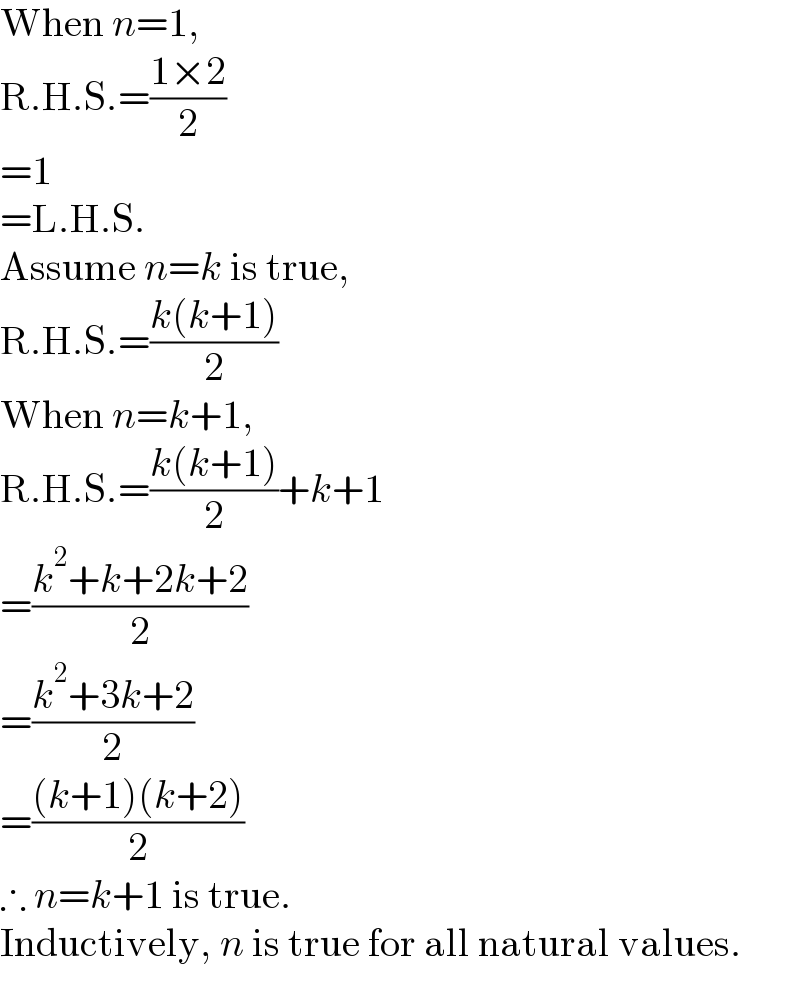
When n=1, R.H.S.=((1×2)/2) =1 =L.H.S. Assume n=k is true, R.H.S.=((k(k+1))/2) When n=k+1, R.H.S.=((k(k+1))/2)+k+1 =((k^2 +k+2k+2)/2) =((k^2 +3k+2)/2) =(((k+1)(k+2))/2) ∴ n=k+1 is true. Inductively, n is true for all natural values.

$$\mathrm{When}\:{n}=\mathrm{1}, \\ $$$$\mathrm{R}.\mathrm{H}.\mathrm{S}.=\frac{\mathrm{1}×\mathrm{2}}{\mathrm{2}} \\ $$$$=\mathrm{1} \\ $$$$=\mathrm{L}.\mathrm{H}.\mathrm{S}. \\ $$$$\mathrm{Assume}\:{n}={k}\:\mathrm{is}\:\mathrm{true}, \\ $$$$\mathrm{R}.\mathrm{H}.\mathrm{S}.=\frac{{k}\left({k}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{When}\:{n}={k}+\mathrm{1}, \\ $$$$\mathrm{R}.\mathrm{H}.\mathrm{S}.=\frac{{k}\left({k}+\mathrm{1}\right)}{\mathrm{2}}+{k}+\mathrm{1} \\ $$$$=\frac{{k}^{\mathrm{2}} +{k}+\mathrm{2}{k}+\mathrm{2}}{\mathrm{2}} \\ $$$$=\frac{{k}^{\mathrm{2}} +\mathrm{3}{k}+\mathrm{2}}{\mathrm{2}} \\ $$$$=\frac{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}{\mathrm{2}} \\ $$$$\therefore\:{n}={k}+\mathrm{1}\:\mathrm{is}\:\mathrm{true}. \\ $$$$\mathrm{Inductively},\:{n}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:\mathrm{natural}\:\mathrm{values}. \\ $$

Answered by MJS_new last updated on 18/Jul/22

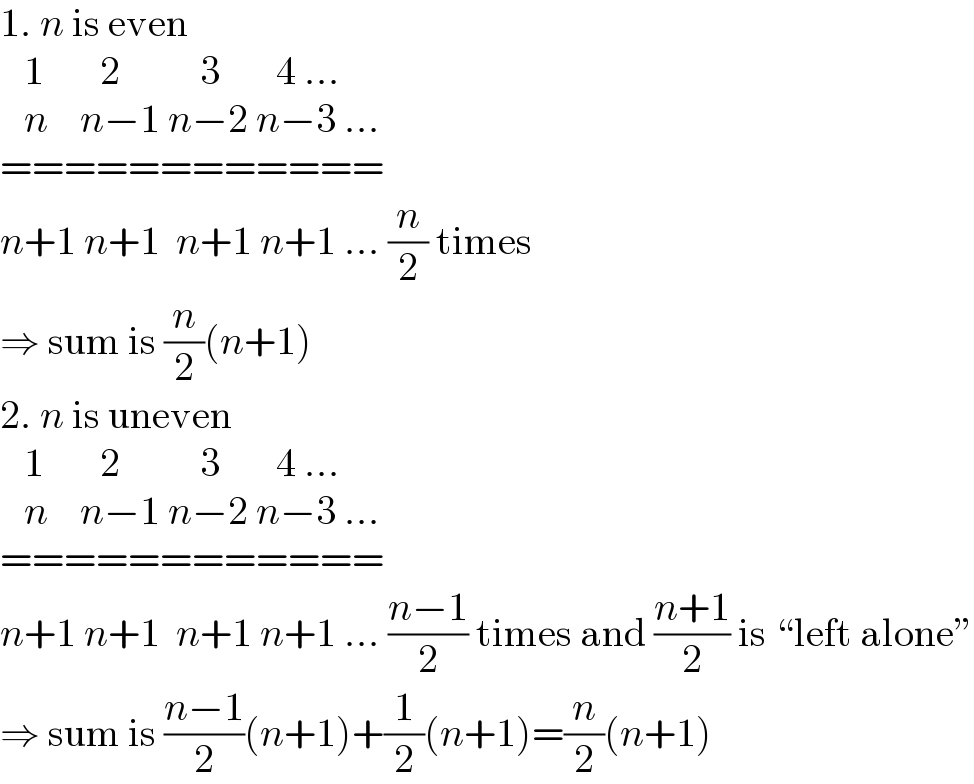
1. n is even 1 2 3 4 ... n n−1 n−2 n−3 ... ============ n+1 n+1 n+1 n+1 ... (n/2) times ⇒ sum is (n/2)(n+1) 2. n is uneven 1 2 3 4 ... n n−1 n−2 n−3 ... ============ n+1 n+1 n+1 n+1 ... ((n−1)/2) times and ((n+1)/2) is “left alone” ⇒ sum is ((n−1)/2)(n+1)+(1/2)(n+1)=(n/2)(n+1)

$$\mathrm{1}.\:{n}\:\mathrm{is}\:\mathrm{even} \\ $$$$\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\mathrm{4}\:… \\ $$$$\:\:\:{n}\:\:\:\:{n}−\mathrm{1}\:{n}−\mathrm{2}\:{n}−\mathrm{3}\:… \\ $$$$============ \\ $$$${n}+\mathrm{1}\:{n}+\mathrm{1}\:\:{n}+\mathrm{1}\:{n}+\mathrm{1}\:…\:\frac{{n}}{\mathrm{2}}\:\mathrm{times} \\ $$$$\Rightarrow\:\mathrm{sum}\:\mathrm{is}\:\frac{{n}}{\mathrm{2}}\left({n}+\mathrm{1}\right) \\ $$$$\mathrm{2}.\:{n}\:\mathrm{is}\:\mathrm{uneven} \\ $$$$\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\mathrm{4}\:… \\ $$$$\:\:\:{n}\:\:\:\:{n}−\mathrm{1}\:{n}−\mathrm{2}\:{n}−\mathrm{3}\:… \\ $$$$============ \\ $$$${n}+\mathrm{1}\:{n}+\mathrm{1}\:\:{n}+\mathrm{1}\:{n}+\mathrm{1}\:…\:\frac{{n}−\mathrm{1}}{\mathrm{2}}\:\mathrm{times}\:\mathrm{and}\:\frac{{n}+\mathrm{1}}{\mathrm{2}}\:\mathrm{is}\:“\mathrm{left}\:\mathrm{alone}'' \\ $$$$\Rightarrow\:\mathrm{sum}\:\mathrm{is}\:\frac{{n}−\mathrm{1}}{\mathrm{2}}\left({n}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left({n}+\mathrm{1}\right)=\frac{{n}}{\mathrm{2}}\left({n}+\mathrm{1}\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply