Menu Close

Question-173834

Tinku Tara 0 Comments
Pin




Question Number 173834 by mnjuly1970 last updated on 19/Jul/22
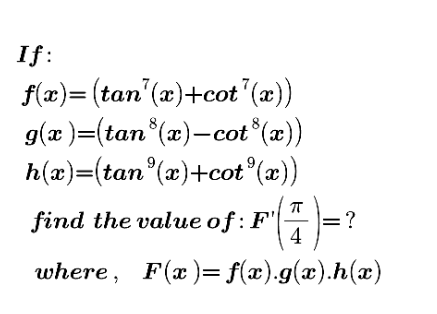
Commented by infinityaction last updated on 20/Jul/22
f(x)g(x)h(x) = (tan^7 x+cot^7 x)(tan^8 x−cot^8 x) × (tan^9 x+cot^9 x) F(x) = (tan^(15) x−cotx+tanx−cot^(15) x)(tan^9 +cot^9 x) F(x)= tan^(24) x−tan^8 x+tan^(10) x−cot^6 x + tan^6 x−cot^(10) x+cot^8 x−cot^(24) x F ′(x) = 24tan^(23) xsec^2 x−8tan^7 xsec^2 x + 10tan^9 xsec^2 x+6cot^5 xcosec^2 x + 6tan^5 xsec^2 x+10cot^9 xcosec^2 x− 8cot^7 xcosec^2 x +24cot^(23) xcosec^2 x F ′(x) = 48−16+20+12+12+20−16+48 F^ ′(x) = 128
$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\boldsymbol{{g}}\left(\boldsymbol{{x}}\right)\boldsymbol{{h}}\left(\boldsymbol{{x}}\right)\:=\:\left(\boldsymbol{\mathrm{tan}}^{\mathrm{7}} \boldsymbol{{x}}+\boldsymbol{\mathrm{cot}}^{\mathrm{7}} \boldsymbol{{x}}\right)\left(\boldsymbol{\mathrm{tan}}^{\mathrm{8}} \boldsymbol{{x}}−\boldsymbol{\mathrm{cot}}^{\mathrm{8}} \boldsymbol{{x}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:×\:\:\left(\boldsymbol{\mathrm{tan}}^{\mathrm{9}} \boldsymbol{{x}}+\boldsymbol{\mathrm{cot}}^{\mathrm{9}} \boldsymbol{{x}}\right) \\ $$$$\:\boldsymbol{{F}}\left(\boldsymbol{{x}}\right)\:=\:\left(\boldsymbol{\mathrm{tan}}^{\mathrm{15}} \boldsymbol{{x}}−\boldsymbol{\mathrm{cot}{x}}+\boldsymbol{\mathrm{tan}{x}}−\boldsymbol{\mathrm{cot}}^{\mathrm{15}} \boldsymbol{{x}}\right)\left(\boldsymbol{\mathrm{tan}}^{\mathrm{9}} +\boldsymbol{\mathrm{cot}}^{\mathrm{9}} \boldsymbol{{x}}\right)\:\:\: \\ $$$$\:\:\:{F}\left({x}\right)=\:\mathrm{tan}^{\mathrm{24}} {x}−\mathrm{tan}^{\mathrm{8}} {x}+\mathrm{tan}^{\mathrm{10}} {x}−\mathrm{cot}^{\mathrm{6}} {x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\:\mathrm{tan}^{\mathrm{6}} {x}−\mathrm{cot}^{\mathrm{10}} {x}+\mathrm{cot}^{\mathrm{8}} {x}−\mathrm{cot}^{\mathrm{24}} {x} \\ $$$${F}\:'\left({x}\right)\:=\:\mathrm{24tan}^{\mathrm{23}} {x}\mathrm{sec}^{\mathrm{2}} {x}−\mathrm{8tan}^{\mathrm{7}} {x}\mathrm{sec}^{\mathrm{2}} {x} \\ $$$$\:\:\:\:\:\:+\:\mathrm{10tan}^{\mathrm{9}} {x}\mathrm{sec}^{\mathrm{2}} {x}+\mathrm{6cot}^{\mathrm{5}} {x}\mathrm{cosec}^{\mathrm{2}} {x} \\ $$$$\:\:\:\:\:\:\:+\:\mathrm{6tan}^{\mathrm{5}} {x}\mathrm{sec}^{\mathrm{2}} {x}+\mathrm{10cot}^{\mathrm{9}} {x}\mathrm{cosec}^{\mathrm{2}} {x}− \\ $$$$\:\:\:\mathrm{8cot}^{\mathrm{7}} {x}\mathrm{cosec}^{\mathrm{2}} {x}\:+\mathrm{24cot}^{\mathrm{23}} {x}\mathrm{cosec}^{\mathrm{2}} {x} \\ $$$${F}\:'\left({x}\right)\:=\:\mathrm{48}−\mathrm{16}+\mathrm{20}+\mathrm{12}+\mathrm{12}+\mathrm{20}−\mathrm{16}+\mathrm{48}\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${F}^{\:} '\left({x}\right)\:=\:\:\:\:\mathrm{128}\:\:\:\:\: \\ $$
Commented by Tawa11 last updated on 19/Jul/22
Great sirs
$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Answered by mahdipoor last updated on 19/Jul/22
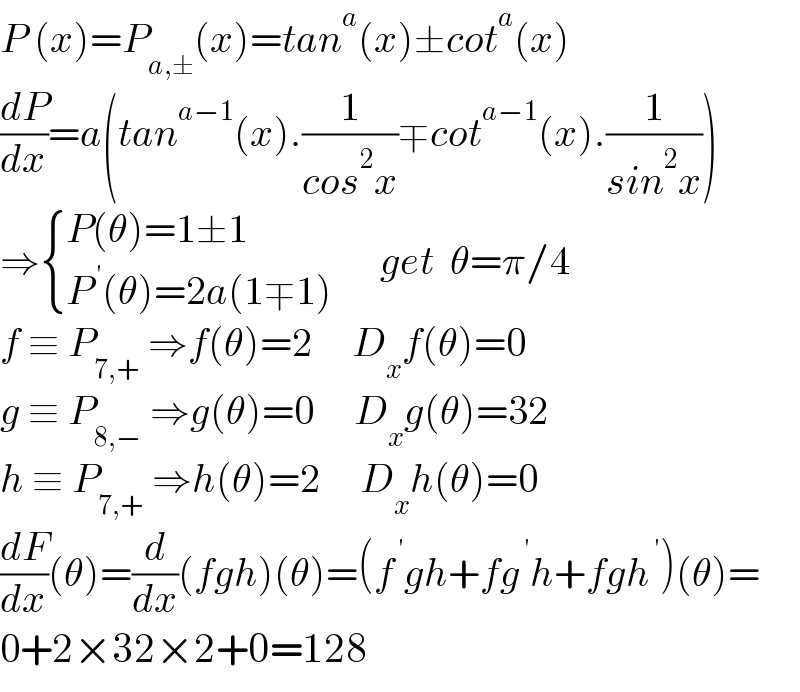
P (x)=P_(a,±) (x)=tan^a (x)±cot^a (x) (dP/dx)=a(tan^(a−1) (x).(1/(cos^2 x))∓cot^(a−1) (x).(1/(sin^2 x))) ⇒ { ((P(θ)=1±1)),((P^( ′) (θ)=2a(1∓1))) :} get θ=π/4 f ≡ P_(7,+) ⇒f(θ)=2 D_x f(θ)=0 g ≡ P_(8,−) ⇒g(θ)=0 D_x g(θ)=32 h ≡ P_(7,+) ⇒h(θ)=2 D_x h(θ)=0 (dF/dx)(θ)=(d/dx)(fgh)(θ)=(f^( ′) gh+fg^( ′) h+fgh^( ′) )(θ)= 0+2×32×2+0=128
$${P}\:\left({x}\right)={P}_{{a},\pm} \left({x}\right)={tan}^{{a}} \left({x}\right)\pm{cot}^{{a}} \left({x}\right) \\ $$$$\frac{{dP}}{{dx}}={a}\left({tan}^{{a}−\mathrm{1}} \left({x}\right).\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}\mp{cot}^{{a}−\mathrm{1}} \left({x}\right).\frac{\mathrm{1}}{{sin}^{\mathrm{2}} {x}}\right) \\ $$$$\Rightarrow\begin{cases}{{P}\left(\theta\right)=\mathrm{1}\pm\mathrm{1}}\\{{P}^{\:'} \left(\theta\right)=\mathrm{2}{a}\left(\mathrm{1}\mp\mathrm{1}\right)}\end{cases}\:\:\:\:\:\:{get}\:\:\theta=\pi/\mathrm{4} \\ $$$${f}\:\equiv\:{P}_{\mathrm{7},+} \:\Rightarrow{f}\left(\theta\right)=\mathrm{2}\:\:\:\:\:{D}_{{x}} {f}\left(\theta\right)=\mathrm{0} \\ $$$${g}\:\equiv\:{P}_{\mathrm{8},−} \:\Rightarrow{g}\left(\theta\right)=\mathrm{0}\:\:\:\:\:{D}_{{x}} {g}\left(\theta\right)=\mathrm{32} \\ $$$${h}\:\equiv\:{P}_{\mathrm{7},+} \:\Rightarrow{h}\left(\theta\right)=\mathrm{2}\:\:\:\:\:{D}_{{x}} {h}\left(\theta\right)=\mathrm{0} \\ $$$$\frac{{dF}}{{dx}}\left(\theta\right)=\frac{{d}}{{dx}}\left({fgh}\right)\left(\theta\right)=\left({f}^{\:'} {gh}+{fg}^{\:'} {h}+{fgh}^{\:'} \right)\left(\theta\right)= \\ $$$$\mathrm{0}+\mathrm{2}×\mathrm{32}×\mathrm{2}+\mathrm{0}=\mathrm{128} \\ $$
Commented by mnjuly1970 last updated on 19/Jul/22
very nice mamnon ostad
$$\:\:\:\:{very}\:{nice}\:\:{mamnon}\:{ostad} \\ $$
Commented by mahdipoor last updated on 20/Jul/22
lotf darid ostad :)
$$\left.{lotf}\:{darid}\:{ostad}\::\right) \\ $$
Answered by mr W last updated on 20/Jul/22
F(x)=f(x)g(x)h(x) ln F(x)=ln f(x)+ln g(x)+ln h(x) ((F′(x))/(F(x)))=((f′(x))/(f(x)))+((g′(x))/(g(x)))+((h′(x))/(h(x))) F′(x)=g(x)h(x)f′(x)+f(x)h(x)g′(x)+f(x)g(x)h′(x) f((π/4))=h((π/4))=2 g((π/4))=0 F′((π/4))=f((π/4))h((π/4))g′((π/4))=4×g′((π/4)) =4×[((8 tan^7 x)/(cos^2 x))+((8 cot^7 x)/(sin^2 x))]_(x=(π/4)) =32×[(1/(1/2))+(1/(1/2))] =32×4=128
$${F}\left({x}\right)={f}\left({x}\right){g}\left({x}\right){h}\left({x}\right) \\ $$$$\mathrm{ln}\:{F}\left({x}\right)=\mathrm{ln}\:{f}\left({x}\right)+\mathrm{ln}\:{g}\left({x}\right)+\mathrm{ln}\:{h}\left({x}\right) \\ $$$$\frac{{F}'\left({x}\right)}{{F}\left({x}\right)}=\frac{{f}'\left({x}\right)}{{f}\left({x}\right)}+\frac{{g}'\left({x}\right)}{{g}\left({x}\right)}+\frac{{h}'\left({x}\right)}{{h}\left({x}\right)} \\ $$$${F}'\left({x}\right)={g}\left({x}\right){h}\left({x}\right){f}'\left({x}\right)+{f}\left({x}\right){h}\left({x}\right){g}'\left({x}\right)+{f}\left({x}\right){g}\left({x}\right){h}'\left({x}\right) \\ $$$${f}\left(\frac{\pi}{\mathrm{4}}\right)={h}\left(\frac{\pi}{\mathrm{4}}\right)=\mathrm{2} \\ $$$${g}\left(\frac{\pi}{\mathrm{4}}\right)=\mathrm{0} \\ $$$${F}'\left(\frac{\pi}{\mathrm{4}}\right)={f}\left(\frac{\pi}{\mathrm{4}}\right){h}\left(\frac{\pi}{\mathrm{4}}\right){g}'\left(\frac{\pi}{\mathrm{4}}\right)=\mathrm{4}×{g}'\left(\frac{\pi}{\mathrm{4}}\right) \\ $$$$=\mathrm{4}×\left[\frac{\mathrm{8}\:\mathrm{tan}^{\mathrm{7}} \:{x}}{\mathrm{cos}^{\mathrm{2}} \:{x}}+\frac{\mathrm{8}\:\mathrm{cot}^{\mathrm{7}} \:{x}}{\mathrm{sin}^{\mathrm{2}} \:{x}}\right]_{{x}=\frac{\pi}{\mathrm{4}}} \\ $$$$=\mathrm{32}×\left[\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}}+\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}}\right] \\ $$$$=\mathrm{32}×\mathrm{4}=\mathrm{128} \\ $$
Commented by mnjuly1970 last updated on 20/Jul/22
really nice solution master
$$\:\:\:{really}\:{nice}\:{solution}\:{master} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *