Question Number 173874 by akolade last updated on 20/Jul/22
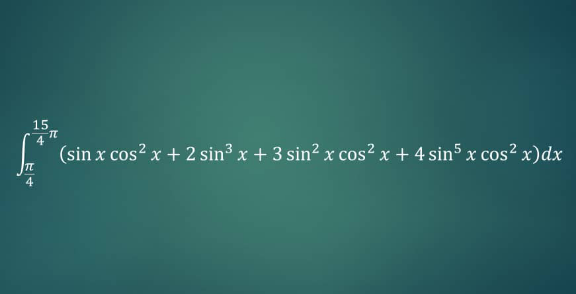
Answered by a.lgnaoui last updated on 21/Jul/22
![I=∫_(π/4) ^(15π/4) (sin xcos^2 x+3sin^2 xcos^2 x+4sin^5 xcos^2 x+2sin^3 x)dx= cos^2 xsin^2 x (3+4sin^3 x)+(sinxcos^2 x+ 2sin^3 x)= (1/4)(sin2x)^2 (3+4sin^3 x)+sinx (1 +sin^2 x )= (3/4)sin^2 (2x)+2sin^3 x+ sinx I=(3/4)∫sin^2 (2x)dx+3∫sin^3 xdx+∫sin xdx ∫sin^2 (2x)dx u′=1⇒u=x v=sin^2 (2x)⇒v′=2sin( 2x)cos(2x)=sin4x ∫sin^2 (2x)dx=[xsin^2 (2x)]−(∫xsin4xdx =[−(1/4)xcos4x]+ sin4x) ⇒∫sin^2 2xdx=xsin^2 2x+(1/4)(xcos4x)−sin 4x ∫(sin^3 x+sinx) dx= ∫sin x(1+sin^2 x)=−cos x(1+sin^2 x)−((cos 2x)/2) I=(3/4)[xsin^2 2x]_(π/4) ^((15π)/4) +(3/(16))[xcos 4x]_(π/4) ^((15π)/4) −(3/4)[ sin4x]_(π/4) ^((15π)/4) − [cos x(1+sin^2 x)]_(π/4) ^((15π)/4) +[((cos 2x)/2)]_(π/4) ^((15π)/4) =(3/4)[ (((15π)/4)sin^2 (−(π/4)) −(π/4)sin^2 (π/4))]+[(3/(16)) (((15π)/4)cos( −π)−(π/4)cos π)]−(3/4)(sin 15π−sin π) −[cos ((π/4))(1+sin^2 (π/4)) − (cos (π/4)(1+sin^2 (π/4) )]+((1/2)cos ((3π)/2)−(1/2)cos (π/2)) I =((−49π)/(32))](https://www.tinkutara.com/question/Q173918.png)
$$\mathrm{I}=\int_{\pi/\mathrm{4}} ^{\mathrm{15}\pi/\mathrm{4}} \left(\mathrm{sin}\:{x}\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{3sin}^{\mathrm{2}} {x}\mathrm{cos}^{\mathrm{2}} {x}+\mathrm{4sin}^{\mathrm{5}} {x}\mathrm{cos}^{\mathrm{2}} {x}+\mathrm{2sin}^{\mathrm{3}} {x}\right){dx}= \\ $$$$\mathrm{cos}^{\mathrm{2}} {x}\mathrm{sin}^{\mathrm{2}} {x}\:\left(\mathrm{3}+\mathrm{4sin}^{\mathrm{3}} {x}\right)+\left(\mathrm{sin}{x}\mathrm{cos}^{\mathrm{2}} {x}+\:\:\mathrm{2sin}^{\mathrm{3}} {x}\right)= \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{sin2}{x}\right)^{\mathrm{2}} \left(\mathrm{3}+\mathrm{4sin}^{\mathrm{3}} {x}\right)+\mathrm{sin}{x}\:\left(\mathrm{1}\:+\mathrm{sin}^{\mathrm{2}} {x}\:\right)= \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)+\mathrm{2sin}^{\mathrm{3}} {x}+\:\mathrm{sin}{x}\: \\ $$$$\:\: \\ $$$$\mathrm{I}=\frac{\mathrm{3}}{\mathrm{4}}\int\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right){dx}+\mathrm{3}\int\mathrm{sin}^{\mathrm{3}} {xdx}+\int\mathrm{sin}\:{xdx} \\ $$$$\int\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{2}{x}\right){dx}\:\:\:\:\:{u}'=\mathrm{1}\Rightarrow{u}={x}\:\:\:\:\:{v}=\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)\Rightarrow{v}'=\mathrm{2sin}\left(\:\mathrm{2}{x}\right)\mathrm{cos}\left(\mathrm{2}{x}\right)=\mathrm{sin4}{x} \\ $$$$\int\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right){dx}=\left[{x}\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)\right]−\left(\int{x}\mathrm{sin4}{xdx}\:\:=\left[−\frac{\mathrm{1}}{\mathrm{4}}{x}\mathrm{cos4}{x}\right]+\:\mathrm{sin4}{x}\right)\:\: \\ $$$$\Rightarrow\int\mathrm{sin}^{\mathrm{2}} \mathrm{2}{xdx}={x}\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{4}}\left({x}\mathrm{cos4}{x}\right)−\mathrm{sin}\:\mathrm{4}{x}\: \\ $$$$\int\left(\mathrm{sin}^{\mathrm{3}} {x}+\mathrm{sin}{x}\right)\:{dx}=\:\int\mathrm{sin}\:{x}\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} {x}\right)=−\mathrm{cos}\:{x}\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} {x}\right)−\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}} \\ $$$$\mathrm{I}=\frac{\mathrm{3}}{\mathrm{4}}\left[{x}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}\right]_{\frac{\pi}{\mathrm{4}}} ^{\frac{\mathrm{15}\pi}{\mathrm{4}}} +\frac{\mathrm{3}}{\mathrm{16}}\left[{x}\mathrm{cos}\:\mathrm{4}{x}\right]_{\frac{\pi}{\mathrm{4}}} ^{\frac{\mathrm{15}\pi}{\mathrm{4}}} \:−\frac{\mathrm{3}}{\mathrm{4}}\left[\:\mathrm{sin4}{x}\right]_{\frac{\pi}{\mathrm{4}}} ^{\frac{\mathrm{15}\pi}{\mathrm{4}}} \\ $$$$\:\:\:−\:\:\:\left[\mathrm{cos}\:{x}\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} {x}\right)\right]_{\frac{\pi}{\mathrm{4}}} ^{\frac{\mathrm{15}\pi}{\mathrm{4}}} +\left[\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}\right]_{\frac{\pi}{\mathrm{4}}} ^{\frac{\mathrm{15}\pi}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\left[\:\left(\frac{\mathrm{15}\pi}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} \left(−\frac{\pi}{\mathrm{4}}\right)\:−\frac{\pi}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{4}}\right)\right]+\left[\frac{\mathrm{3}}{\mathrm{16}}\:\left(\frac{\mathrm{15}\pi}{\mathrm{4}}\mathrm{cos}\left(\:−\pi\right)−\frac{\pi}{\mathrm{4}}\mathrm{cos}\:\pi\right)\right]−\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{sin}\:\mathrm{15}\pi−\mathrm{sin}\:\pi\right) \\ $$$$\:\:\:\:−\left[\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}\right)\left(\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \frac{\pi}{\mathrm{4}}\right)\:−\:\left(\mathrm{cos}\:\frac{\pi}{\mathrm{4}}\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{4}}\:\right)\right]+\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\frac{\pi}{\mathrm{2}}\right)\right. \\ $$$$\:\:\:\mathrm{I}\:\:\:=\frac{−\mathrm{49}\pi}{\mathrm{32}} \\ $$
