Question Number 173923 by mathlove last updated on 21/Jul/22

Commented by Rasheed.Sindhi last updated on 21/Jul/22
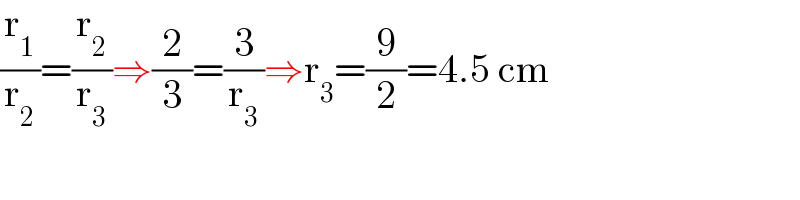
$$\frac{\mathrm{r}_{\mathrm{1}} }{\mathrm{r}_{\mathrm{2}} }=\frac{\mathrm{r}_{\mathrm{2}} }{\mathrm{r}_{\mathrm{3}} }\Rightarrow\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{3}}{\mathrm{r}_{\mathrm{3}} }\Rightarrow\mathrm{r}_{\mathrm{3}} =\frac{\mathrm{9}}{\mathrm{2}}=\mathrm{4}.\mathrm{5}\:\mathrm{cm} \\ $$
Answered by mr W last updated on 21/Jul/22
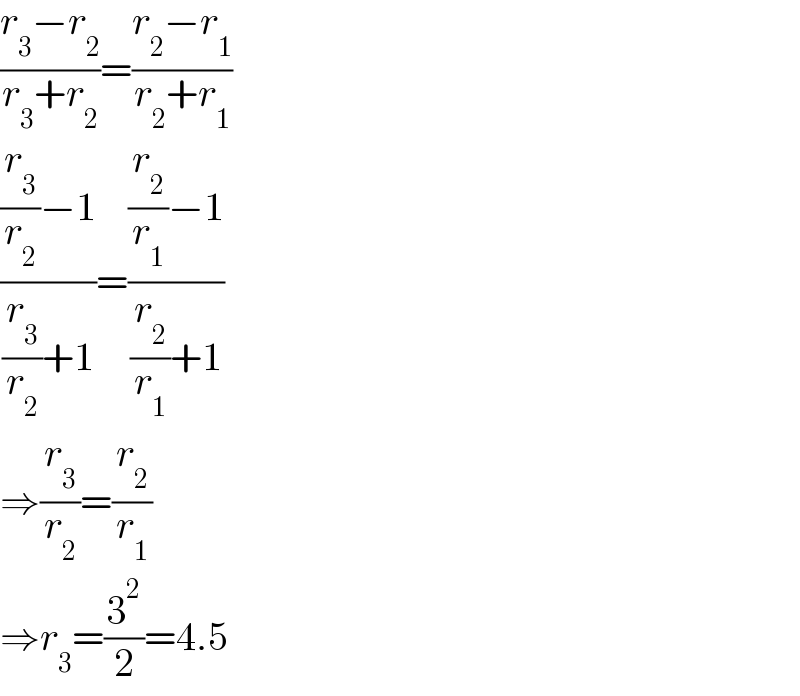
$$\frac{{r}_{\mathrm{3}} −{r}_{\mathrm{2}} }{{r}_{\mathrm{3}} +{r}_{\mathrm{2}} }=\frac{{r}_{\mathrm{2}} −{r}_{\mathrm{1}} }{{r}_{\mathrm{2}} +{r}_{\mathrm{1}} } \\ $$$$\frac{\frac{{r}_{\mathrm{3}} }{{r}_{\mathrm{2}} }−\mathrm{1}}{\frac{{r}_{\mathrm{3}} }{{r}_{\mathrm{2}} }+\mathrm{1}}=\frac{\frac{{r}_{\mathrm{2}} }{{r}_{\mathrm{1}} }−\mathrm{1}}{\frac{{r}_{\mathrm{2}} }{{r}_{\mathrm{1}} }+\mathrm{1}} \\ $$$$\Rightarrow\frac{{r}_{\mathrm{3}} }{{r}_{\mathrm{2}} }=\frac{{r}_{\mathrm{2}} }{{r}_{\mathrm{1}} } \\ $$$$\Rightarrow{r}_{\mathrm{3}} =\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{4}.\mathrm{5} \\ $$
Commented by Tawa11 last updated on 21/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by peter frank last updated on 21/Jul/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mathlove last updated on 22/Jul/22

$${thanks}\:{for}\:{all} \\ $$
