Question-173970

Question Number 173970 by mnjuly1970 last updated on 22/Jul/22

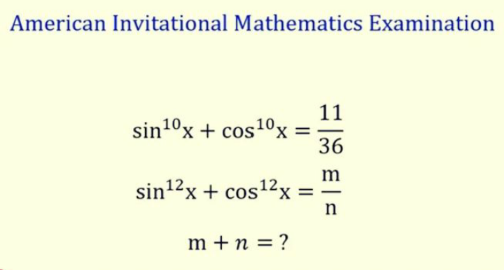
Commented by Tawa11 last updated on 22/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Commented by infinityaction last updated on 22/Jul/22

sin^(12) x + cos^(12) x = (m/n) = p let y = sin^2 x y^5 + (1−y)^(5 ) = ((11)/(36)) if we let t = (1/2)−y ((1/2)+t)^5 +((1/2)−t)^5 = ((11)/(36)) use binomial theorem (1/(16))(80t^4 +40t^2 +1) = ((11)/(36)) t^2 = (1/(12)) ⇒t = ±(1/(2(√3))) ((1/2)−t)^6 +((1/2)+t)^6 = p use binomial theorem p = ((13)/(54)) = (m/n) m+n = 67

$$\:\:\:\:\:\:\:\mathrm{sin}^{\mathrm{12}} {x}\:+\:\mathrm{cos}^{\mathrm{12}} {x}\:\:=\:\frac{{m}}{{n}}\:\:=\:\:{p}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{let}\:{y}\:=\:\mathrm{sin}^{\mathrm{2}} {x} \\ $$$$\:\:\:\:\:\:\:\:{y}^{\mathrm{5}} \:+\:\left(\mathrm{1}−{y}\right)^{\mathrm{5}\:} \:=\:\:\frac{\mathrm{11}}{\mathrm{36}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{if}\:{we}\:{let}\:\:\:\:{t}\:=\:\frac{\mathrm{1}}{\mathrm{2}}−{y} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\frac{\mathrm{1}}{\mathrm{2}}+{t}\right)^{\mathrm{5}} +\left(\frac{\mathrm{1}}{\mathrm{2}}−{t}\right)^{\mathrm{5}} \:=\:\:\frac{\mathrm{11}}{\mathrm{36}} \\ $$$$\:\:\:\:\:\:\:\:\:{use}\:{binomial}\:{theorem} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{80}{t}^{\mathrm{4}} +\mathrm{40}{t}^{\mathrm{2}} +\mathrm{1}\right)\:=\:\frac{\mathrm{11}}{\mathrm{36}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{t}^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{12}}\:\Rightarrow{t}\:\:=\:\:\pm\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\frac{\mathrm{1}}{\mathrm{2}}−{t}\right)^{\mathrm{6}} +\left(\frac{\mathrm{1}}{\mathrm{2}}+{t}\right)^{\mathrm{6}} \:=\:\:{p} \\ $$$$\:\:\:\:\:\:\:{use}\:{binomial}\:{theorem} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{p}\:\:=\:\:\frac{\mathrm{13}}{\mathrm{54}}\:=\:\frac{{m}}{{n}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{m}+{n}\:=\:\mathrm{67} \\ $$

Commented by mnjuly1970 last updated on 22/Jul/22

$${grateful}\:{sir}\: \\ $$

Answered by mr W last updated on 22/Jul/22

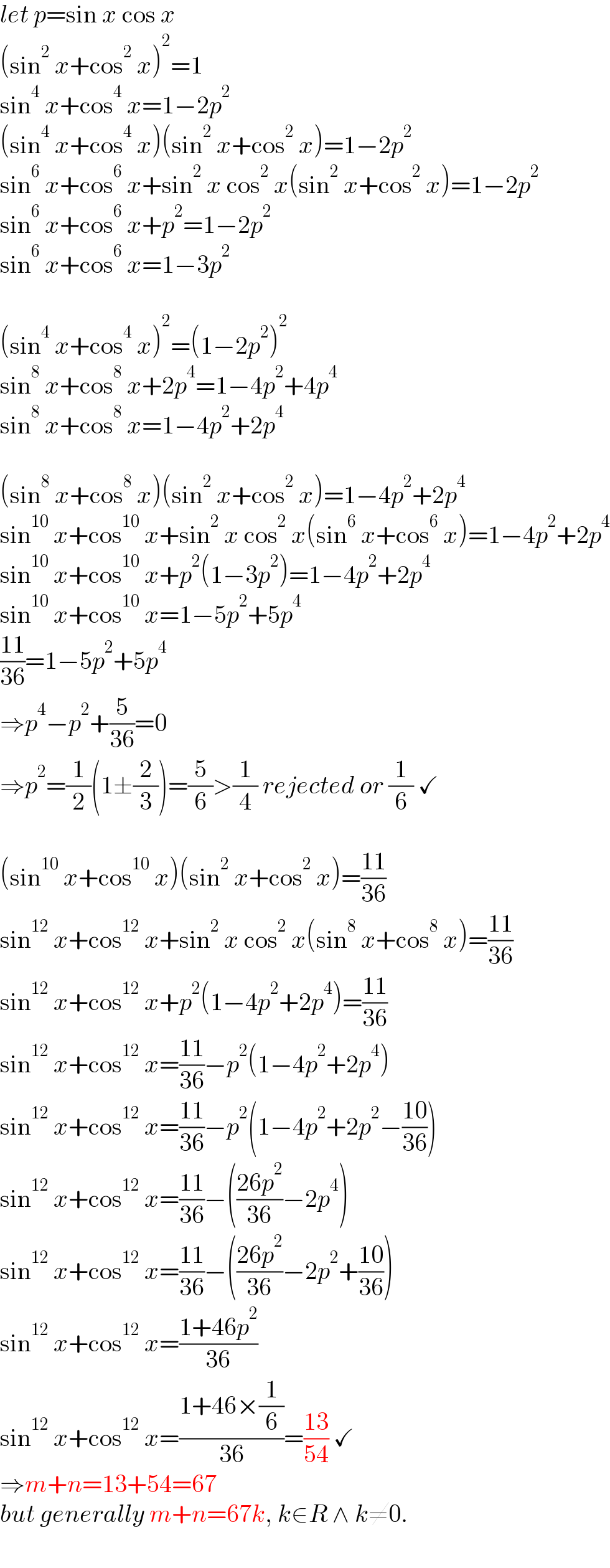
let p=sin x cos x (sin^2 x+cos^2 x)^2 =1 sin^4 x+cos^4 x=1−2p^2 (sin^4 x+cos^4 x)(sin^2 x+cos^2 x)=1−2p^2 sin^6 x+cos^6 x+sin^2 x cos^2 x(sin^2 x+cos^2 x)=1−2p^2 sin^6 x+cos^6 x+p^2 =1−2p^2 sin^6 x+cos^6 x=1−3p^2 (sin^4 x+cos^4 x)^2 =(1−2p^2 )^2 sin^8 x+cos^8 x+2p^4 =1−4p^2 +4p^4 sin^8 x+cos^8 x=1−4p^2 +2p^4 (sin^8 x+cos^8 x)(sin^2 x+cos^2 x)=1−4p^2 +2p^4 sin^(10) x+cos^(10) x+sin^2 x cos^2 x(sin^6 x+cos^6 x)=1−4p^2 +2p^4 sin^(10) x+cos^(10) x+p^2 (1−3p^2 )=1−4p^2 +2p^4 sin^(10) x+cos^(10) x=1−5p^2 +5p^4 ((11)/(36))=1−5p^2 +5p^4 ⇒p^4 −p^2 +(5/(36))=0 ⇒p^2 =(1/2)(1±(2/3))=(5/6)>(1/4) rejected or (1/6) ✓ (sin^(10) x+cos^(10) x)(sin^2 x+cos^2 x)=((11)/(36)) sin^(12) x+cos^(12) x+sin^2 x cos^2 x(sin^8 x+cos^8 x)=((11)/(36)) sin^(12) x+cos^(12) x+p^2 (1−4p^2 +2p^4 )=((11)/(36)) sin^(12) x+cos^(12) x=((11)/(36))−p^2 (1−4p^2 +2p^4 ) sin^(12) x+cos^(12) x=((11)/(36))−p^2 (1−4p^2 +2p^2 −((10)/(36))) sin^(12) x+cos^(12) x=((11)/(36))−(((26p^2 )/(36))−2p^4 ) sin^(12) x+cos^(12) x=((11)/(36))−(((26p^2 )/(36))−2p^2 +((10)/(36))) sin^(12) x+cos^(12) x=((1+46p^2 )/(36)) sin^(12) x+cos^(12) x=((1+46×(1/6))/(36))=((13)/(54)) ✓ ⇒m+n=13+54=67 but generally m+n=67k, k∈R ∧ k≠0.

$${let}\:{p}=\mathrm{sin}\:{x}\:\mathrm{cos}\:{x} \\ $$$$\left(\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{cos}^{\mathrm{2}} \:{x}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{sin}^{\mathrm{4}} \:{x}+\mathrm{cos}^{\mathrm{4}} \:{x}=\mathrm{1}−\mathrm{2}{p}^{\mathrm{2}} \\ $$$$\left(\mathrm{sin}^{\mathrm{4}} \:{x}+\mathrm{cos}^{\mathrm{4}} \:{x}\right)\left(\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{cos}^{\mathrm{2}} \:{x}\right)=\mathrm{1}−\mathrm{2}{p}^{\mathrm{2}} \\ $$$$\mathrm{sin}^{\mathrm{6}} \:{x}+\mathrm{cos}^{\mathrm{6}} \:{x}+\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{cos}^{\mathrm{2}} \:{x}\left(\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{cos}^{\mathrm{2}} \:{x}\right)=\mathrm{1}−\mathrm{2}{p}^{\mathrm{2}} \\ $$$$\mathrm{sin}^{\mathrm{6}} \:{x}+\mathrm{cos}^{\mathrm{6}} \:{x}+{p}^{\mathrm{2}} =\mathrm{1}−\mathrm{2}{p}^{\mathrm{2}} \\ $$$$\mathrm{sin}^{\mathrm{6}} \:{x}+\mathrm{cos}^{\mathrm{6}} \:{x}=\mathrm{1}−\mathrm{3}{p}^{\mathrm{2}} \\ $$$$ \\ $$$$\left(\mathrm{sin}^{\mathrm{4}} \:{x}+\mathrm{cos}^{\mathrm{4}} \:{x}\right)^{\mathrm{2}} =\left(\mathrm{1}−\mathrm{2}{p}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\mathrm{sin}^{\mathrm{8}} \:{x}+\mathrm{cos}^{\mathrm{8}} \:{x}+\mathrm{2}{p}^{\mathrm{4}} =\mathrm{1}−\mathrm{4}{p}^{\mathrm{2}} +\mathrm{4}{p}^{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{8}} \:{x}+\mathrm{cos}^{\mathrm{8}} \:{x}=\mathrm{1}−\mathrm{4}{p}^{\mathrm{2}} +\mathrm{2}{p}^{\mathrm{4}} \\ $$$$ \\ $$$$\left(\mathrm{sin}^{\mathrm{8}} \:{x}+\mathrm{cos}^{\mathrm{8}} \:{x}\right)\left(\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{cos}^{\mathrm{2}} \:{x}\right)=\mathrm{1}−\mathrm{4}{p}^{\mathrm{2}} +\mathrm{2}{p}^{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{10}} \:{x}+\mathrm{cos}^{\mathrm{10}} \:{x}+\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{cos}^{\mathrm{2}} \:{x}\left(\mathrm{sin}^{\mathrm{6}} \:{x}+\mathrm{cos}^{\mathrm{6}} \:{x}\right)=\mathrm{1}−\mathrm{4}{p}^{\mathrm{2}} +\mathrm{2}{p}^{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{10}} \:{x}+\mathrm{cos}^{\mathrm{10}} \:{x}+{p}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{3}{p}^{\mathrm{2}} \right)=\mathrm{1}−\mathrm{4}{p}^{\mathrm{2}} +\mathrm{2}{p}^{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{10}} \:{x}+\mathrm{cos}^{\mathrm{10}} \:{x}=\mathrm{1}−\mathrm{5}{p}^{\mathrm{2}} +\mathrm{5}{p}^{\mathrm{4}} \\ $$$$\frac{\mathrm{11}}{\mathrm{36}}=\mathrm{1}−\mathrm{5}{p}^{\mathrm{2}} +\mathrm{5}{p}^{\mathrm{4}} \\ $$$$\Rightarrow{p}^{\mathrm{4}} −{p}^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{36}}=\mathrm{0} \\ $$$$\Rightarrow{p}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\pm\frac{\mathrm{2}}{\mathrm{3}}\right)=\frac{\mathrm{5}}{\mathrm{6}}>\frac{\mathrm{1}}{\mathrm{4}}\:{rejected}\:{or}\:\frac{\mathrm{1}}{\mathrm{6}}\:\checkmark \\ $$$$ \\ $$$$\left(\mathrm{sin}^{\mathrm{10}} \:{x}+\mathrm{cos}^{\mathrm{10}} \:{x}\right)\left(\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{cos}^{\mathrm{2}} \:{x}\right)=\frac{\mathrm{11}}{\mathrm{36}} \\ $$$$\mathrm{sin}^{\mathrm{12}} \:{x}+\mathrm{cos}^{\mathrm{12}} \:{x}+\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{cos}^{\mathrm{2}} \:{x}\left(\mathrm{sin}^{\mathrm{8}} \:{x}+\mathrm{cos}^{\mathrm{8}} \:{x}\right)=\frac{\mathrm{11}}{\mathrm{36}} \\ $$$$\mathrm{sin}^{\mathrm{12}} \:{x}+\mathrm{cos}^{\mathrm{12}} \:{x}+{p}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{4}{p}^{\mathrm{2}} +\mathrm{2}{p}^{\mathrm{4}} \right)=\frac{\mathrm{11}}{\mathrm{36}} \\ $$$$\mathrm{sin}^{\mathrm{12}} \:{x}+\mathrm{cos}^{\mathrm{12}} \:{x}=\frac{\mathrm{11}}{\mathrm{36}}−{p}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{4}{p}^{\mathrm{2}} +\mathrm{2}{p}^{\mathrm{4}} \right) \\ $$$$\mathrm{sin}^{\mathrm{12}} \:{x}+\mathrm{cos}^{\mathrm{12}} \:{x}=\frac{\mathrm{11}}{\mathrm{36}}−{p}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{4}{p}^{\mathrm{2}} +\mathrm{2}{p}^{\mathrm{2}} −\frac{\mathrm{10}}{\mathrm{36}}\right) \\ $$$$\mathrm{sin}^{\mathrm{12}} \:{x}+\mathrm{cos}^{\mathrm{12}} \:{x}=\frac{\mathrm{11}}{\mathrm{36}}−\left(\frac{\mathrm{26}{p}^{\mathrm{2}} }{\mathrm{36}}−\mathrm{2}{p}^{\mathrm{4}} \right) \\ $$$$\mathrm{sin}^{\mathrm{12}} \:{x}+\mathrm{cos}^{\mathrm{12}} \:{x}=\frac{\mathrm{11}}{\mathrm{36}}−\left(\frac{\mathrm{26}{p}^{\mathrm{2}} }{\mathrm{36}}−\mathrm{2}{p}^{\mathrm{2}} +\frac{\mathrm{10}}{\mathrm{36}}\right) \\ $$$$\mathrm{sin}^{\mathrm{12}} \:{x}+\mathrm{cos}^{\mathrm{12}} \:{x}=\frac{\mathrm{1}+\mathrm{46}{p}^{\mathrm{2}} }{\mathrm{36}} \\ $$$$\mathrm{sin}^{\mathrm{12}} \:{x}+\mathrm{cos}^{\mathrm{12}} \:{x}=\frac{\mathrm{1}+\mathrm{46}×\frac{\mathrm{1}}{\mathrm{6}}}{\mathrm{36}}=\frac{\mathrm{13}}{\mathrm{54}}\:\checkmark \\ $$$$\Rightarrow{m}+{n}=\mathrm{13}+\mathrm{54}=\mathrm{67} \\ $$$${but}\:{generally}\:{m}+{n}=\mathrm{67}{k},\:{k}\in{R}\:\wedge\:{k}\neq\mathrm{0}. \\ $$

Commented by Tawa11 last updated on 22/Jul/22