Question Number 173981 by AgniMath last updated on 22/Jul/22
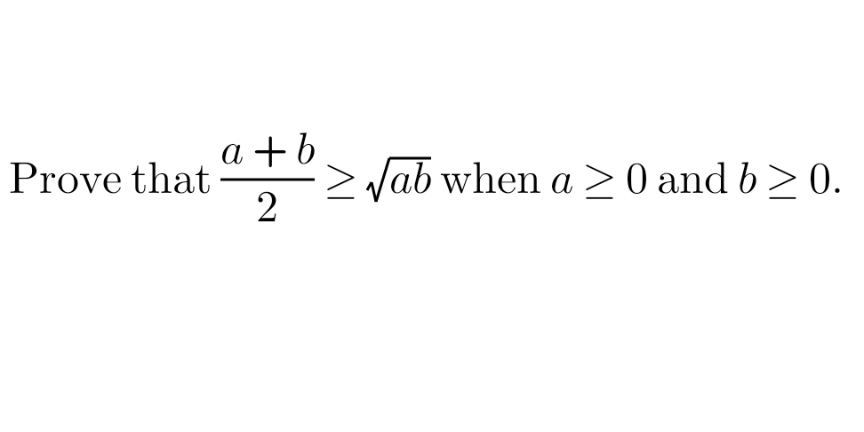
Answered by Frix last updated on 22/Jul/22
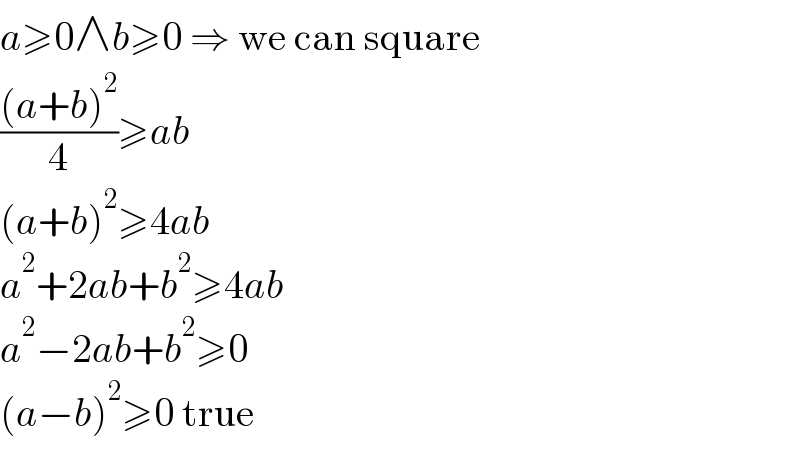
$${a}\geqslant\mathrm{0}\wedge{b}\geqslant\mathrm{0}\:\Rightarrow\:\mathrm{we}\:\mathrm{can}\:\mathrm{square} \\ $$$$\frac{\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{4}}\geqslant{ab} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} \geqslant\mathrm{4}{ab} \\ $$$${a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} \geqslant\mathrm{4}{ab} \\ $$$${a}^{\mathrm{2}} −\mathrm{2}{ab}+{b}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\left({a}−{b}\right)^{\mathrm{2}} \geqslant\mathrm{0}\:\mathrm{true} \\ $$
Answered by puissant last updated on 22/Jul/22
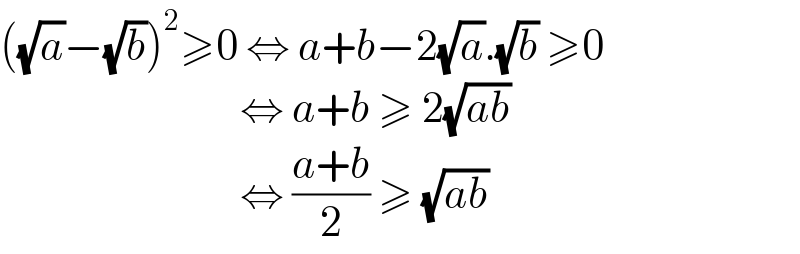
$$\left(\sqrt{{a}}−\sqrt{{b}}\right)^{\mathrm{2}} \geqslant\mathrm{0}\:\Leftrightarrow\:{a}+{b}−\mathrm{2}\sqrt{{a}}.\sqrt{{b}}\:\geqslant\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Leftrightarrow\:{a}+{b}\:\geqslant\:\mathrm{2}\sqrt{{ab}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Leftrightarrow\:\frac{{a}+{b}}{\mathrm{2}}\:\geqslant\:\sqrt{{ab}} \\ $$
