Question Number 173992 by dragan91 last updated on 22/Jul/22

Commented by mr W last updated on 22/Jul/22
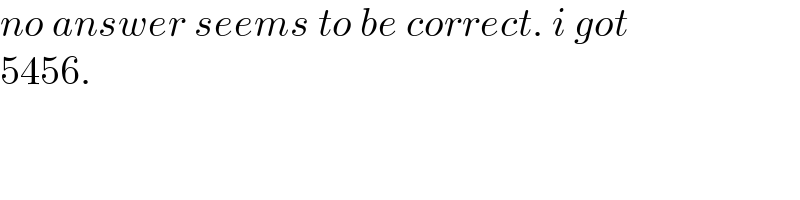
$${no}\:{answer}\:{seems}\:{to}\:{be}\:{correct}.\:{i}\:{got} \\ $$$$\mathrm{5456}. \\ $$
Answered by mr W last updated on 22/Jul/22
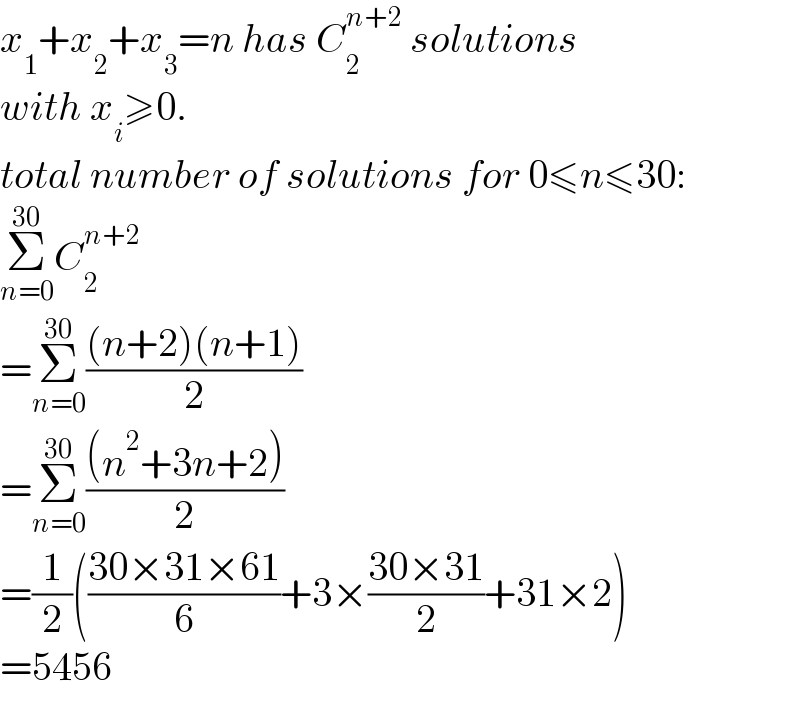
$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} ={n}\:{has}\:{C}_{\mathrm{2}} ^{{n}+\mathrm{2}} \:{solutions} \\ $$$${with}\:{x}_{{i}} \geqslant\mathrm{0}. \\ $$$${total}\:{number}\:{of}\:{solutions}\:{for}\:\mathrm{0}\leqslant{n}\leqslant\mathrm{30}: \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\mathrm{30}} {\sum}}{C}_{\mathrm{2}} ^{{n}+\mathrm{2}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\mathrm{30}} {\sum}}\frac{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\mathrm{30}} {\sum}}\frac{\left({n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{2}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{30}×\mathrm{31}×\mathrm{61}}{\mathrm{6}}+\mathrm{3}×\frac{\mathrm{30}×\mathrm{31}}{\mathrm{2}}+\mathrm{31}×\mathrm{2}\right) \\ $$$$=\mathrm{5456} \\ $$
Commented by dragan91 last updated on 22/Jul/22
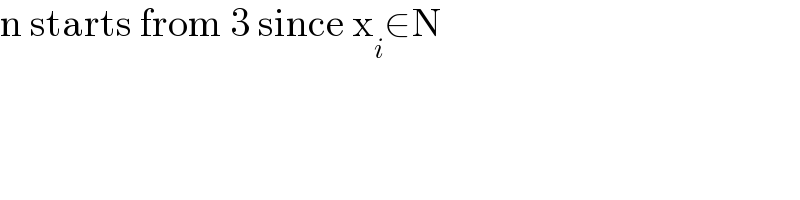
$$\mathrm{n}\:\mathrm{starts}\:\mathrm{from}\:\mathrm{3}\:\mathrm{since}\:\mathrm{x}_{{i}} \in\mathrm{N} \\ $$
Commented by dragan91 last updated on 22/Jul/22
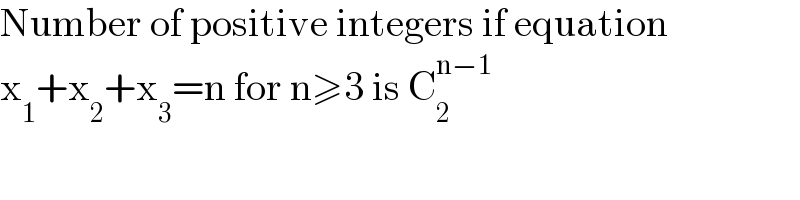
$$\mathrm{Number}\:\mathrm{of}\:\mathrm{positive}\:\mathrm{integers}\:\mathrm{if}\:\mathrm{equation} \\ $$$$\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} +\mathrm{x}_{\mathrm{3}} =\mathrm{n}\:\mathrm{for}\:\mathrm{n}\geqslant\mathrm{3}\:\mathrm{is}\:\mathrm{C}_{\mathrm{2}} ^{\mathrm{n}−\mathrm{1}} \\ $$$$ \\ $$
Commented by dragan91 last updated on 22/Jul/22

$$\mathrm{At}\:\mathrm{first}\:\mathrm{I}\:\mathrm{get}\:\mathrm{4060} \\ $$
Commented by mr W last updated on 22/Jul/22
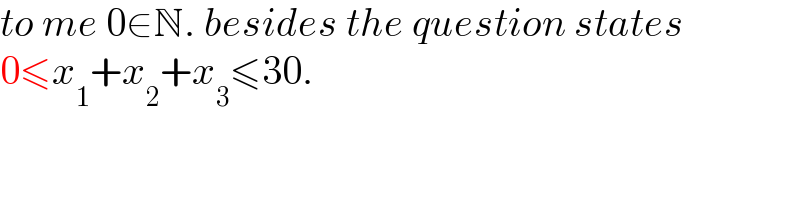
$${to}\:{me}\:\mathrm{0}\in\mathbb{N}.\:{besides}\:{the}\:{question}\:{states} \\ $$$$\mathrm{0}\leqslant{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} \leqslant\mathrm{30}. \\ $$
Commented by mr W last updated on 22/Jul/22

Commented by dragan91 last updated on 22/Jul/22

$$\mathrm{Ok}.\mathrm{For}\:\mathrm{me}\:\mathrm{0}\:\mathrm{is}\:\mathrm{not}\:\mathrm{natural}.\:\mathrm{I}\:\mathrm{will}\:\mathrm{check}\:\mathrm{with} \\ $$$$\mathrm{other}\:\mathrm{people}.\:\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{given}\:\mathrm{answers}\:\mathrm{is}\:\mathrm{all}\:\mathrm{wrong}.\:\mathrm{Thanks}. \\ $$$$ \\ $$
Commented by Tawa11 last updated on 22/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 22/Jul/22

$${it}\:{is}\:{just}\:{a}\:{question}\:{of}\:{definition} \\ $$$${if}\:\mathrm{0}\:{is}\:{a}\:{natural}\:{number}\:{or}\:{not}. \\ $$$${in}\:{Germany}\:{it}'{s}\:{even}\:{differently} \\ $$$${defined}\:{in}\:{different}\:{federal}\:{states}. \\ $$
Commented by dragan91 last updated on 22/Jul/22

$$\mathrm{thanks} \\ $$
Commented by MJS_new last updated on 23/Jul/22
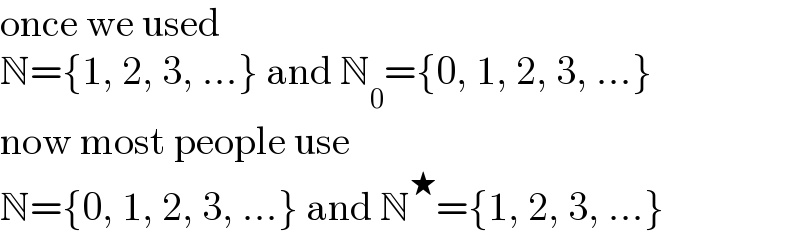
$$\mathrm{once}\:\mathrm{we}\:\mathrm{used} \\ $$$$\mathbb{N}=\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:…\right\}\:\mathrm{and}\:\mathbb{N}_{\mathrm{0}} =\left\{\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:…\right\} \\ $$$$\mathrm{now}\:\mathrm{most}\:\mathrm{people}\:\mathrm{use} \\ $$$$\mathbb{N}=\left\{\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:…\right\}\:\mathrm{and}\:\mathbb{N}^{\bigstar} =\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:…\right\} \\ $$
