Question Number 173993 by AgniMath last updated on 22/Jul/22
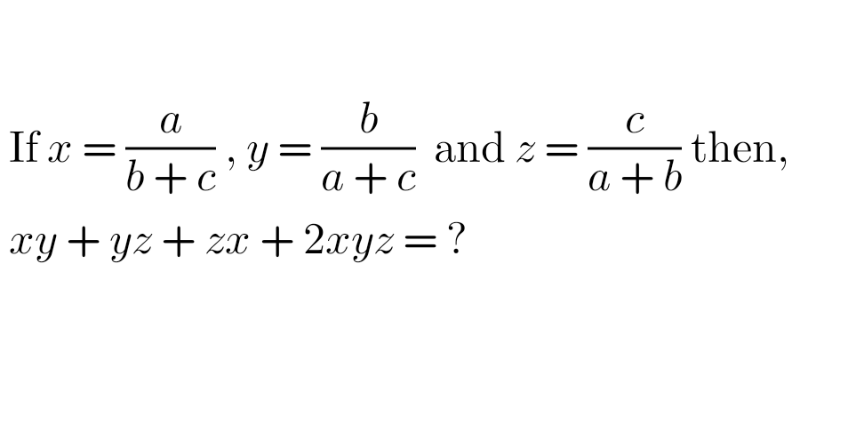
Answered by som(math1967) last updated on 22/Jul/22

$$\:{xy}+{yz}+{zx}+\mathrm{2}{xyz} \\ $$$$=\frac{{ab}}{\left({b}+{c}\right)\left({c}+{a}\right)}\:+\frac{{bc}}{\left({c}+{a}\right)\left({a}+{b}\right)} \\ $$$$\:\:+\frac{{ca}}{\left({a}+{b}\right)\left({b}+{c}\right)}+\frac{\mathrm{2}{abc}}{\left({a}+{b}\right)\left({b}+{c}\right)\left({c}+{a}\right)} \\ $$$$=\frac{{ab}\left({a}+{b}\right)+{bc}\left({b}+{c}\right)+{ca}\left({c}+{a}\right)+\mathrm{2}{abc}}{\left({a}+{b}\right)\left({b}+{c}\right)\left({c}+{a}\right)} \\ $$$$=\frac{\left({a}+{b}\right)\left({b}+{c}\right)\left({c}+{a}\right)}{\left({a}+{b}\right)\left({b}+{c}\right)\left({c}+{a}\right)}\:\:\:\:\:\bigstar \\ $$$$=\mathrm{1} \\ $$$$\bigstar{ab}\left({a}+{b}\right)+{b}^{\mathrm{2}} {c}+{bc}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}+{ca}^{\mathrm{2}} +\mathrm{2}{abc} \\ $$$$={ab}\left({a}+{b}\right)+{c}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\right)+{c}^{\mathrm{2}} \left({a}+{b}\right) \\ $$$$={ab}\left({a}+{b}\right)+{c}\left({a}+{b}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} \left({a}+{b}\right) \\ $$$$=\left({a}+{b}\right)\left({ab}+{ca}+{bc}+{c}^{\mathrm{2}} \right) \\ $$$$=\left({a}+{b}\right)\left({b}+{c}\right)\left({c}+{a}\right) \\ $$
Commented by Tawa11 last updated on 23/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
