Menu Close

Question-174023

Tinku Tara 0 Comments
Pin




Question Number 174023 by dragan91 last updated on 22/Jul/22
Commented by dragan91 last updated on 23/Jul/22
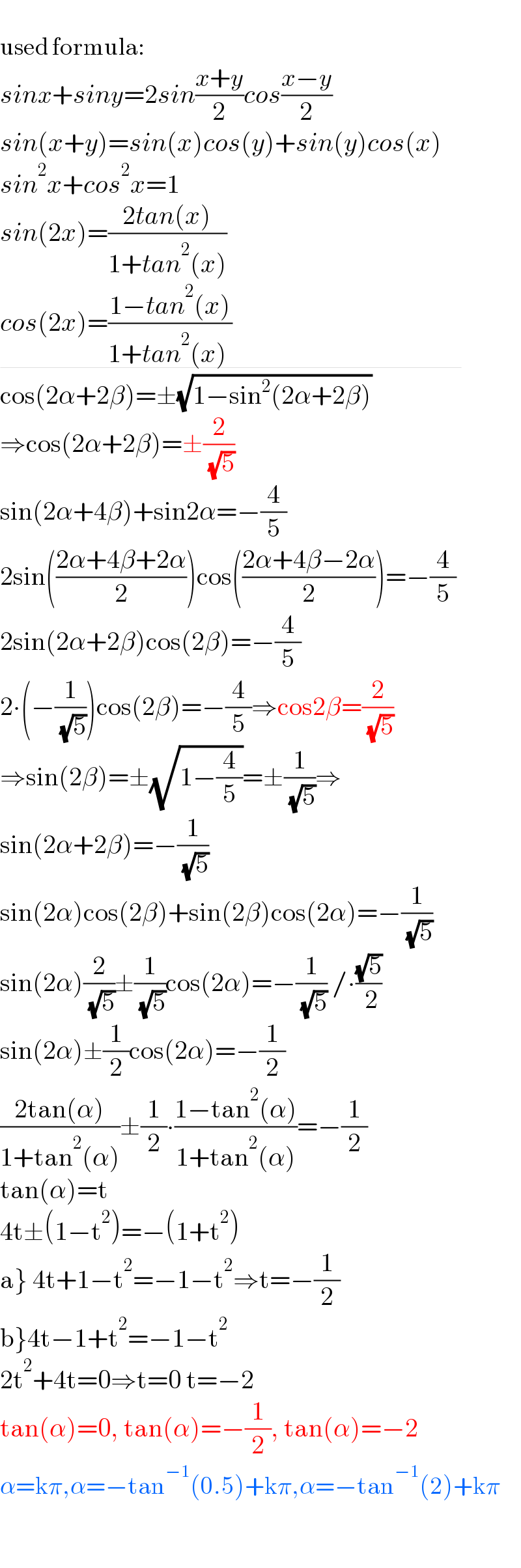
used formula: sinx+siny=2sin((x+y)/2)cos((x−y)/2) sin(x+y)=sin(x)cos(y)+sin(y)cos(x) sin^2 x+cos^2 x=1 sin(2x)=((2tan(x))/(1+tan^2 (x))) cos(2x)=((1−tan^2 (x))/(1+tan^2 (x) )) cos(2α+2β)=±(√(1−sin^2 (2α+2β))) ⇒cos(2α+2β)=±(2/( (√5))) sin(2α+4β)+sin2α=−(4/5) 2sin(((2α+4β+2α)/2))cos(((2α+4β−2α)/2))=−(4/5) 2sin(2α+2β)cos(2β)=−(4/5) 2∙(−(1/( (√5))))cos(2β)=−(4/5)⇒cos2β=(2/( (√5))) ⇒sin(2β)=±(√(1−(4/5)))=±(1/( (√5)))⇒ sin(2α+2β)=−(1/( (√5))) sin(2α)cos(2β)+sin(2β)cos(2α)=−(1/( (√5))) sin(2α)(2/( (√5)))±(1/( (√5)))cos(2α)=−(1/( (√5))) /∙((√5)/( 2)) sin(2α)±(1/2)cos(2α)=−(1/2) ((2tan(α))/(1+tan^2 (α)))±(1/2)∙((1−tan^2 (α))/(1+tan^2 (α)))=−(1/2) tan(α)=t 4t±(1−t^2 )=−(1+t^2 ) a} 4t+1−t^2 =−1−t^2 ⇒t=−(1/2) b}4t−1+t^2 =−1−t^2 2t^2 +4t=0⇒t=0 t=−2 tan(α)=0, tan(α)=−(1/2), tan(α)=−2 α=kπ,α=−tan^(−1) (0.5)+kπ,α=−tan^(−1) (2)+kπ
$$ \\ $$$$\mathrm{used}\:\mathrm{formula}: \\ $$$${sinx}+{siny}=\mathrm{2}{sin}\frac{{x}+{y}}{\mathrm{2}}{cos}\frac{{x}−{y}}{\mathrm{2}} \\ $$$${sin}\left({x}+{y}\right)={sin}\left({x}\right){cos}\left({y}\right)+{sin}\left({y}\right){cos}\left({x}\right) \\ $$$${sin}^{\mathrm{2}} {x}+{cos}^{\mathrm{2}} {x}=\mathrm{1} \\ $$$${sin}\left(\mathrm{2}{x}\right)=\frac{\mathrm{2}{tan}\left({x}\right)}{\mathrm{1}+{tan}^{\mathrm{2}} \left({x}\right)} \\ $$$$\underline{{cos}\left(\mathrm{2}{x}\right)=\frac{\mathrm{1}−{tan}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}+{tan}^{\mathrm{2}} \left({x}\right)\:}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} \\ $$$$\mathrm{cos}\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)=\pm\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}\alpha+\mathrm{2}\beta\right)} \\ $$$$\Rightarrow\mathrm{cos}\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)=\pm\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}} \\ $$$$\mathrm{sin}\left(\mathrm{2}\alpha+\mathrm{4}\beta\right)+\mathrm{sin2}\alpha=−\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{2sin}\left(\frac{\mathrm{2}\alpha+\mathrm{4}\beta+\mathrm{2}\alpha}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{2}\alpha+\mathrm{4}\beta−\mathrm{2}\alpha}{\mathrm{2}}\right)=−\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{2sin}\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)\mathrm{cos}\left(\mathrm{2}\beta\right)=−\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{2}\centerdot\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)\mathrm{cos}\left(\mathrm{2}\beta\right)=−\frac{\mathrm{4}}{\mathrm{5}}\Rightarrow\mathrm{cos2}\beta=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow\mathrm{sin}\left(\mathrm{2}\beta\right)=\pm\sqrt{\mathrm{1}−\frac{\mathrm{4}}{\mathrm{5}}}=\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\Rightarrow \\ $$$$\mathrm{sin}\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\mathrm{sin}\left(\mathrm{2}\alpha\right)\mathrm{cos}\left(\mathrm{2}\beta\right)+\mathrm{sin}\left(\mathrm{2}\beta\right)\mathrm{cos}\left(\mathrm{2}\alpha\right)=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\mathrm{sin}\left(\mathrm{2}\alpha\right)\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\mathrm{cos}\left(\mathrm{2}\alpha\right)=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:/\centerdot\frac{\sqrt{\mathrm{5}}}{\:\mathrm{2}} \\ $$$$\mathrm{sin}\left(\mathrm{2}\alpha\right)\pm\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{2}\alpha\right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{2tan}\left(\alpha\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\alpha\right)}\pm\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \left(\alpha\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\alpha\right)}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{tan}\left(\alpha\right)=\mathrm{t} \\ $$$$\mathrm{4t}\pm\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)=−\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right) \\ $$$$\left.\mathrm{a}\right\}\:\mathrm{4t}+\mathrm{1}−\mathrm{t}^{\mathrm{2}} =−\mathrm{1}−\mathrm{t}^{\mathrm{2}} \Rightarrow\mathrm{t}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left.\mathrm{b}\right\}\mathrm{4t}−\mathrm{1}+\mathrm{t}^{\mathrm{2}} =−\mathrm{1}−\mathrm{t}^{\mathrm{2}} \\ $$$$\mathrm{2t}^{\mathrm{2}} +\mathrm{4t}=\mathrm{0}\Rightarrow\mathrm{t}=\mathrm{0}\:\mathrm{t}=−\mathrm{2} \\ $$$$\mathrm{tan}\left(\alpha\right)=\mathrm{0},\:\mathrm{tan}\left(\alpha\right)=−\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{tan}\left(\alpha\right)=−\mathrm{2} \\ $$$$\alpha=\mathrm{k}\pi,\alpha=−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{0}.\mathrm{5}\right)+\mathrm{k}\pi,\alpha=−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)+\mathrm{k}\pi \\ $$$$ \\ $$
Answered by behi834171 last updated on 23/Jul/22
let use:s,for:sin and,c,for:cos sinp+sinq=2sin((p+q)/2)cos((q−p)/2) ⇒s(2a+4b)+s2a=2s((2a+4b+2a)/2).c((2a−2a−4b)/2)= =2s(2a+2b).c2b [cos(−2b)=cos2b] ⇒2×((−1)/( (√5)))×c2b=−(4/5)⇒c2b=(2/( (√5))),s2b=(1/( (√5))) s2a.c2b+c2a.s2b=−(1/( (√5)))[ { ((sin2a=((2tga)/(1+tg^2 a)))),((cos2a=((1−tg^2 a)/(1+tg^2 a)))) :} ⇒^(tga=x) ((2x)/(1+x^2 )).(2/( (√5)))+((1−x^2 )/(1+x^2 )).(1/( (√5)))=−(1/( (√5)))⇒ 4x+1−x^2 =−1−x^2 ⇒4x=−2⇒x=tg𝛂=−(1/2) .■
$${let}\:{use}:{s},{for}:{sin}\:{and},{c},{for}:{cos} \\ $$$${sinp}+{sinq}=\mathrm{2}{sin}\frac{{p}+{q}}{\mathrm{2}}{cos}\frac{{q}−{p}}{\mathrm{2}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{s}}\left(\mathrm{2}\boldsymbol{\mathrm{a}}+\mathrm{4}\boldsymbol{\mathrm{b}}\right)+\boldsymbol{\mathrm{s}}\mathrm{2}\boldsymbol{\mathrm{a}}=\mathrm{2}\boldsymbol{\mathrm{s}}\frac{\mathrm{2}\boldsymbol{\mathrm{a}}+\mathrm{4}\boldsymbol{\mathrm{b}}+\mathrm{2}\boldsymbol{\mathrm{a}}}{\mathrm{2}}.\boldsymbol{\mathrm{c}}\frac{\mathrm{2}\boldsymbol{\mathrm{a}}−\mathrm{2}\boldsymbol{\mathrm{a}}−\mathrm{4}\boldsymbol{\mathrm{b}}}{\mathrm{2}}= \\ $$$$=\mathrm{2}\boldsymbol{\mathrm{s}}\left(\mathrm{2}\boldsymbol{\mathrm{a}}+\mathrm{2}\boldsymbol{\mathrm{b}}\right).\boldsymbol{\mathrm{c}}\mathrm{2}\boldsymbol{\mathrm{b}}\:\:\:\:\:\left[\boldsymbol{\mathrm{cos}}\left(−\mathrm{2}\boldsymbol{\mathrm{b}}\right)=\boldsymbol{\mathrm{cos}}\mathrm{2}\boldsymbol{\mathrm{b}}\right] \\ $$$$\Rightarrow\mathrm{2}×\frac{−\mathrm{1}}{\:\sqrt{\mathrm{5}}}×{c}\mathrm{2}{b}=−\frac{\mathrm{4}}{\mathrm{5}}\Rightarrow\boldsymbol{\mathrm{c}}\mathrm{2}\boldsymbol{\mathrm{b}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}},\boldsymbol{\mathrm{s}}\mathrm{2}\boldsymbol{\mathrm{b}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\boldsymbol{\mathrm{s}}\mathrm{2}\boldsymbol{\mathrm{a}}.\boldsymbol{\mathrm{c}}\mathrm{2}\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{c}}\mathrm{2}\boldsymbol{\mathrm{a}}.\boldsymbol{\mathrm{s}}\mathrm{2}\boldsymbol{\mathrm{b}}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left[\begin{cases}{\boldsymbol{\mathrm{sin}}\mathrm{2}\boldsymbol{\mathrm{a}}=\frac{\mathrm{2}\boldsymbol{\mathrm{tga}}}{\mathrm{1}+\boldsymbol{\mathrm{tg}}^{\mathrm{2}} \boldsymbol{\mathrm{a}}}}\\{\boldsymbol{\mathrm{cos}}\mathrm{2}\boldsymbol{\mathrm{a}}=\frac{\mathrm{1}−\boldsymbol{\mathrm{tg}}^{\mathrm{2}} \boldsymbol{\mathrm{a}}}{\mathrm{1}+\boldsymbol{\mathrm{tg}}^{\mathrm{2}} \boldsymbol{\mathrm{a}}}}\end{cases}\right. \\ $$$$\overset{\boldsymbol{\mathrm{tga}}=\boldsymbol{\mathrm{x}}} {\Rightarrow}\:\:\:\:\frac{\mathrm{2}\boldsymbol{\mathrm{x}}}{\mathrm{1}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} }.\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}+\frac{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{1}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} }.\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\Rightarrow \\ $$$$\mathrm{4}\boldsymbol{\mathrm{x}}+\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} =−\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} \Rightarrow\mathrm{4}\boldsymbol{\mathrm{x}}=−\mathrm{2}\Rightarrow\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{tg}\alpha}=−\frac{\mathrm{1}}{\mathrm{2}}\:.\blacksquare \\ $$$$ \\ $$
Commented by Tawa11 last updated on 23/Jul/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 23/Jul/22
sin (2α+2β)=−(1/( (√5))) cos (2α+2β)=±(2/( (√5))) sin (4α+4β)=2×(−(1/( (√5))))(±(2/( (√5))))=∓(4/5) cos (4α+4β)=1−2×(−(1/( (√5))))^2 =(3/5) sin (4α+4β−2α)+sin (2α)=−(4/5) sin (4α+4β) cos (2α)−cos (4α+4β) sin (2α)+sin (2α)=−(4/5) (∓(4/5)) cos (2α)−((3/5)) sin (2α)+sin (2α)=−(4/5) sin (2α)∓2 cos (2α)=−2 ((2 tan α)/(1+tan^2 α))∓2×((1−tan^2 α)/(1+tan^2 α))=−2 let t=tan α (t/(1+t^2 ))∓((1−t^2 )/(1+t^2 ))=−1 1+t^2 +t∓(1−t^2 )=0 1+t^2 +t−1+t^2 =0 2t^2 +t=0 ⇒t=0 or −(1/2) 1+t^2 +t+1−t^2 =0 t+2=0 ⇒t=−2 ⇒tan α=0 ∨ −(1/2) ∨ −2 ∨ ±∞ ⇒α=kπ, kπ−tan^(−1) (1/2), kπ−tan^(−1) 2, kπ−(π/2)
$$\mathrm{sin}\:\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\mathrm{cos}\:\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)=\pm\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}} \\ $$$$\mathrm{sin}\:\left(\mathrm{4}\alpha+\mathrm{4}\beta\right)=\mathrm{2}×\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)\left(\pm\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right)=\mp\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{cos}\:\left(\mathrm{4}\alpha+\mathrm{4}\beta\right)=\mathrm{1}−\mathrm{2}×\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$ \\ $$$$\mathrm{sin}\:\left(\mathrm{4}\alpha+\mathrm{4}\beta−\mathrm{2}\alpha\right)+\mathrm{sin}\:\left(\mathrm{2}\alpha\right)=−\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{sin}\:\left(\mathrm{4}\alpha+\mathrm{4}\beta\right)\:\mathrm{cos}\:\left(\mathrm{2}\alpha\right)−\mathrm{cos}\:\left(\mathrm{4}\alpha+\mathrm{4}\beta\right)\:\mathrm{sin}\:\left(\mathrm{2}\alpha\right)+\mathrm{sin}\:\left(\mathrm{2}\alpha\right)=−\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\left(\mp\frac{\mathrm{4}}{\mathrm{5}}\right)\:\mathrm{cos}\:\left(\mathrm{2}\alpha\right)−\left(\frac{\mathrm{3}}{\mathrm{5}}\right)\:\mathrm{sin}\:\left(\mathrm{2}\alpha\right)+\mathrm{sin}\:\left(\mathrm{2}\alpha\right)=−\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{sin}\:\left(\mathrm{2}\alpha\right)\mp\mathrm{2}\:\mathrm{cos}\:\left(\mathrm{2}\alpha\right)=−\mathrm{2} \\ $$$$ \\ $$$$\frac{\mathrm{2}\:\mathrm{tan}\:\alpha}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha}\mp\mathrm{2}×\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\alpha}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha}=−\mathrm{2} \\ $$$${let}\:{t}=\mathrm{tan}\:\alpha \\ $$$$\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\mp\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }=−\mathrm{1} \\ $$$$\mathrm{1}+{t}^{\mathrm{2}} +{t}\mp\left(\mathrm{1}−{t}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{1}+{t}^{\mathrm{2}} +{t}−\mathrm{1}+{t}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{2}{t}^{\mathrm{2}} +{t}=\mathrm{0}\:\Rightarrow{t}=\mathrm{0}\:{or}\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{1}+{t}^{\mathrm{2}} +{t}+\mathrm{1}−{t}^{\mathrm{2}} =\mathrm{0} \\ $$$${t}+\mathrm{2}=\mathrm{0}\:\Rightarrow{t}=−\mathrm{2} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\mathrm{0}\:\vee\:−\frac{\mathrm{1}}{\mathrm{2}}\:\vee\:−\mathrm{2}\:\vee\:\pm\infty \\ $$$$\Rightarrow\alpha={k}\pi,\:{k}\pi−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}},\:{k}\pi−\mathrm{tan}^{−\mathrm{1}} \mathrm{2},\:{k}\pi−\frac{\pi}{\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 23/Jul/22
Great sirs
$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Commented by dragan91 last updated on 23/Jul/22
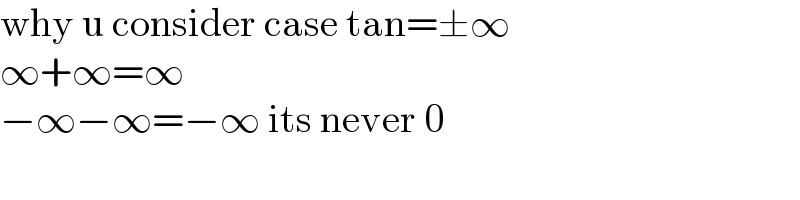
why u consider case tan=±∞ ∞+∞=∞ −∞−∞=−∞ its never 0
$$\mathrm{why}\:\mathrm{u}\:\mathrm{consider}\:\mathrm{case}\:\mathrm{tan}=\pm\infty \\ $$$$\infty+\infty=\infty \\ $$$$−\infty−\infty=−\infty\:\mathrm{its}\:\mathrm{never}\:\mathrm{0} \\ $$
Commented by mr W last updated on 23/Jul/22
(t/(1+t^2 ))+((1−t^2 )/(1+t^2 ))=−1 ⇒((t+2)/(1+t^2 ))=0 ⇒t=−2 or t=±∞
$$\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }=−\mathrm{1} \\ $$$$\Rightarrow\frac{{t}+\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow{t}=−\mathrm{2}\:{or}\:{t}=\pm\infty \\ $$
Commented by mr W last updated on 23/Jul/22
Commented by mr W last updated on 23/Jul/22
check: eqn. 1 and eqn. 2 intersect at four points. that means there are four solutions for α: α=kπ α=kπ−tan^(−1) (1/2) α=kπ−tan^(−1) 2 α=kπ−(π/2)
$${check}: \\ $$$${eqn}.\:\mathrm{1}\:{and}\:{eqn}.\:\mathrm{2}\:{intersect}\:{at}\:{four} \\ $$$${points}.\:{that}\:{means}\:{there}\:{are}\:{four} \\ $$$${solutions}\:{for}\:\alpha: \\ $$$$\alpha={k}\pi \\ $$$$\alpha={k}\pi−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\alpha={k}\pi−\mathrm{tan}^{−\mathrm{1}} \mathrm{2} \\ $$$$\alpha={k}\pi−\frac{\pi}{\mathrm{2}} \\ $$
Commented by MJS_new last updated on 24/Jul/22
I get tan β =2−(√5) ∧ (tan α =−2 ∨ tan α =0) by simply substituting u=tan α ∧ v=tan β which leads to { ((−((2(u+v)(uv−1))/((u^2 +1)(v^2 +1)))=−((√5)/5))),((((4(u+v)(uv−1)(v−1)(v+1))/((u^2 +1)^2 (v^2 +1)^2 ))=−(4/5))) :} both are only square in u { ((u^2 −((10(v−1)(v+1))/( (√5)v^2 −10v+(√5)))u+(((√5)v^2 +10v+(√5))/( (√5)v^2 −10v+(√5)))=0)),((u^2 +((5(v−1)^2 (v+1)^2 )/((v^2 +v−1)(v^2 +4v−1)))u+(((v^2 −v−1)(v^2 −4v−1))/((v^2 +v−1)(vv^2 +4v+1)))=0)) :} subtracting and solving I get (1) u=((2v)/(v^2 −1)) ∨ (2) v=2−(√5) (1) gives no real solution
$$\mathrm{I}\:\mathrm{get} \\ $$$$\mathrm{tan}\:\beta\:=\mathrm{2}−\sqrt{\mathrm{5}}\:\wedge\:\left(\mathrm{tan}\:\alpha\:=−\mathrm{2}\:\vee\:\mathrm{tan}\:\alpha\:=\mathrm{0}\right) \\ $$$$\mathrm{by}\:\mathrm{simply}\:\mathrm{substituting} \\ $$$${u}=\mathrm{tan}\:\alpha\:\wedge\:{v}=\mathrm{tan}\:\beta \\ $$$$\mathrm{which}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\begin{cases}{−\frac{\mathrm{2}\left({u}+{v}\right)\left({uv}−\mathrm{1}\right)}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)\left({v}^{\mathrm{2}} +\mathrm{1}\right)}=−\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}}\\{\frac{\mathrm{4}\left({u}+{v}\right)\left({uv}−\mathrm{1}\right)\left({v}−\mathrm{1}\right)\left({v}+\mathrm{1}\right)}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left({v}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{4}}{\mathrm{5}}}\end{cases} \\ $$$$\mathrm{both}\:\mathrm{are}\:\mathrm{only}\:\mathrm{square}\:\mathrm{in}\:{u} \\ $$$$\begin{cases}{{u}^{\mathrm{2}} −\frac{\mathrm{10}\left({v}−\mathrm{1}\right)\left({v}+\mathrm{1}\right)}{\:\sqrt{\mathrm{5}}{v}^{\mathrm{2}} −\mathrm{10}{v}+\sqrt{\mathrm{5}}}{u}+\frac{\sqrt{\mathrm{5}}{v}^{\mathrm{2}} +\mathrm{10}{v}+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{5}}{v}^{\mathrm{2}} −\mathrm{10}{v}+\sqrt{\mathrm{5}}}=\mathrm{0}}\\{{u}^{\mathrm{2}} +\frac{\mathrm{5}\left({v}−\mathrm{1}\right)^{\mathrm{2}} \left({v}+\mathrm{1}\right)^{\mathrm{2}} }{\left({v}^{\mathrm{2}} +{v}−\mathrm{1}\right)\left({v}^{\mathrm{2}} +\mathrm{4}{v}−\mathrm{1}\right)}{u}+\frac{\left({v}^{\mathrm{2}} −{v}−\mathrm{1}\right)\left({v}^{\mathrm{2}} −\mathrm{4}{v}−\mathrm{1}\right)}{\left({v}^{\mathrm{2}} +{v}−\mathrm{1}\right)\left({vv}^{\mathrm{2}} +\mathrm{4}{v}+\mathrm{1}\right)}=\mathrm{0}}\end{cases} \\ $$$$\mathrm{subtracting}\:\mathrm{and}\:\mathrm{solving}\:\mathrm{I}\:\mathrm{get} \\ $$$$\left(\mathrm{1}\right)\:{u}=\frac{\mathrm{2}{v}}{{v}^{\mathrm{2}} −\mathrm{1}}\:\vee\:\left(\mathrm{2}\right)\:{v}=\mathrm{2}−\sqrt{\mathrm{5}} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{gives}\:\mathrm{no}\:\mathrm{real}\:\mathrm{solution} \\ $$
Commented by peter frank last updated on 24/Jul/22
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *