Question-174071

Question Number 174071 by alcohol last updated on 24/Jul/22

Answered by aleks041103 last updated on 24/Jul/22

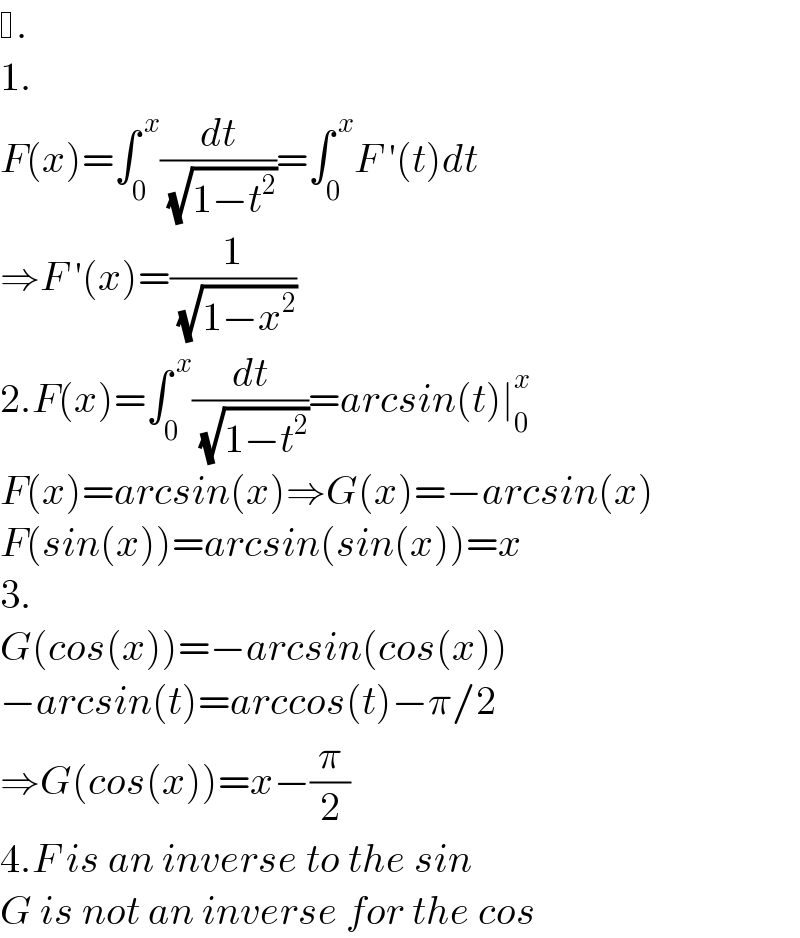
. 1. F(x)=∫_0 ^( x) (dt/( (√(1−t^2 ))))=∫_0 ^( x) F ′(t)dt ⇒F ′(x)=(1/( (√(1−x^2 )))) 2.F(x)=∫_0 ^( x) (dt/( (√(1−t^2 ))))=arcsin(t)∣_0 ^x F(x)=arcsin(x)⇒G(x)=−arcsin(x) F(sin(x))=arcsin(sin(x))=x 3. G(cos(x))=−arcsin(cos(x)) −arcsin(t)=arccos(t)−π/2 ⇒G(cos(x))=x−(π/2) 4.F is an inverse to the sin G is not an inverse for the cos

$$ . \\ $$$$\mathrm{1}. \\ $$$${F}\left({x}\right)=\int_{\mathrm{0}} ^{\:{x}} \frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=\int_{\mathrm{0}} ^{\:{x}} {F}\:'\left({t}\right){dt} \\ $$$$\Rightarrow{F}\:'\left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\mathrm{2}.{F}\left({x}\right)=\int_{\mathrm{0}} ^{\:{x}} \frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}={arcsin}\left({t}\right)\mid_{\mathrm{0}} ^{{x}} \\ $$$${F}\left({x}\right)={arcsin}\left({x}\right)\Rightarrow{G}\left({x}\right)=−{arcsin}\left({x}\right) \\ $$$${F}\left({sin}\left({x}\right)\right)={arcsin}\left({sin}\left({x}\right)\right)={x} \\ $$$$\mathrm{3}. \\ $$$${G}\left({cos}\left({x}\right)\right)=−{arcsin}\left({cos}\left({x}\right)\right) \\ $$$$−{arcsin}\left({t}\right)={arccos}\left({t}\right)−\pi/\mathrm{2} \\ $$$$\Rightarrow{G}\left({cos}\left({x}\right)\right)={x}−\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{4}.{F}\:{is}\:{an}\:{inverse}\:{to}\:{the}\:{sin} \\ $$$${G}\:{is}\:{not}\:{an}\:{inverse}\:{for}\:{the}\:{cos} \\ $$

Answered by CElcedricjunior last updated on 25/Jul/22

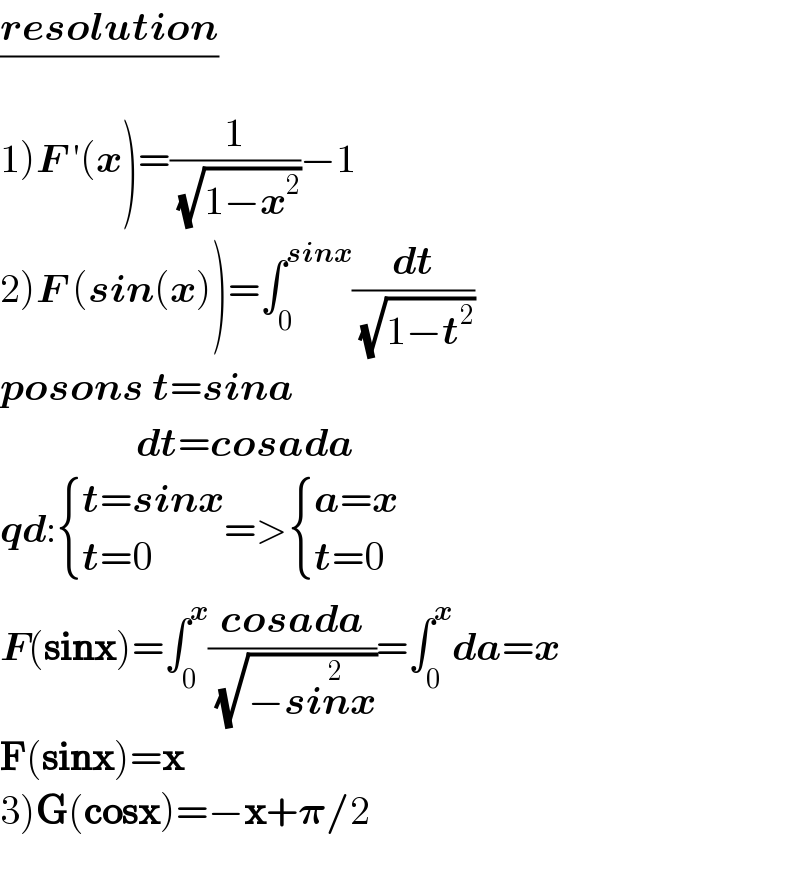
((resolution)/) 1)F ′(x)=(1/( (√(1−x^2 ))))−1 2)F (sin(x))=∫_0 ^(sinx) (dt/( (√(1−t^2 )))) posons t=sina dt=cosada qd: { ((t=sinx)),((t=0)) :}=> { ((a=x)),((t=0)) :} F(sinx)=∫_0 ^x ((cosada)/( (√(−sin^2 x))))=∫_0 ^x da=x F(sinx)=x 3)G(cosx)=−x+𝛑/2

$$\frac{\boldsymbol{{resolution}}}{} \\ $$$$\left.\mathrm{1}\right)\boldsymbol{{F}}\:'\left(\boldsymbol{{x}}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }}−\mathrm{1} \\ $$$$\left.\mathrm{2}\right)\boldsymbol{{F}}\:\left(\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)\right)=\int_{\mathrm{0}} ^{\boldsymbol{{sinx}}} \frac{\boldsymbol{{dt}}}{\:\sqrt{\mathrm{1}−\boldsymbol{{t}}^{\mathrm{2}} }} \\ $$$$\boldsymbol{{posons}}\:\boldsymbol{{t}}=\boldsymbol{{sina}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{dt}}=\boldsymbol{{cosada}} \\ $$$$\boldsymbol{{qd}}:\begin{cases}{\boldsymbol{{t}}=\boldsymbol{{sinx}}}\\{\boldsymbol{{t}}=\mathrm{0}}\end{cases}=>\begin{cases}{\boldsymbol{{a}}=\boldsymbol{{x}}}\\{\boldsymbol{{t}}=\mathrm{0}}\end{cases} \\ $$$$\boldsymbol{{F}}\left(\boldsymbol{\mathrm{sinx}}\right)=\int_{\mathrm{0}} ^{\boldsymbol{{x}}} \frac{\boldsymbol{{cosada}}}{\:\sqrt{−\boldsymbol{{si}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}}}=\int_{\mathrm{0}} ^{\boldsymbol{{x}}} \boldsymbol{{da}}=\boldsymbol{{x}} \\ $$$$\boldsymbol{\mathrm{F}}\left(\boldsymbol{\mathrm{sinx}}\right)=\boldsymbol{\mathrm{x}} \\ $$$$\left.\mathrm{3}\right)\boldsymbol{\mathrm{G}}\left(\boldsymbol{\mathrm{cosx}}\right)=−\boldsymbol{\mathrm{x}}+\boldsymbol{\pi}/\mathrm{2} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply