Question-174084

Question Number 174084 by AgniMath last updated on 24/Jul/22

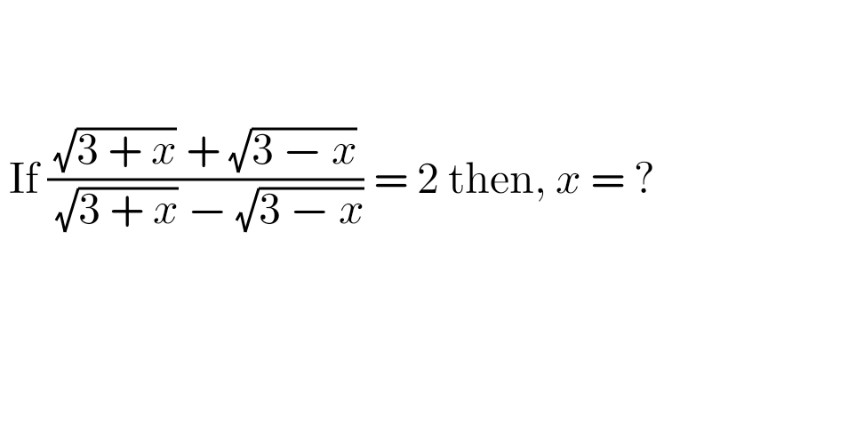
Commented by infinityaction last updated on 24/Jul/22

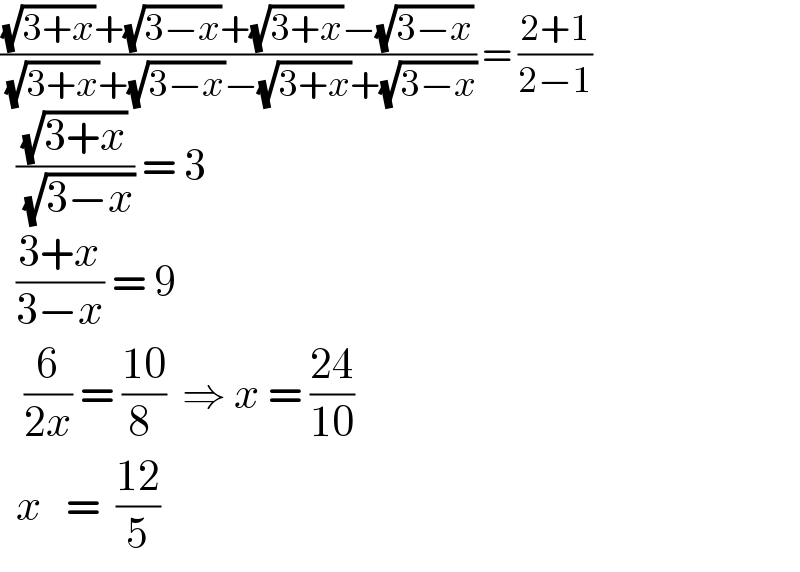
(((√(3+x))+(√(3−x))+(√(3+x))−(√(3−x)))/( (√(3+x))+(√(3−x))−(√(3+x))+(√(3−x)))) = ((2+1)/(2−1)) ((√(3+x))/( (√(3−x)))) = 3 ((3+x)/(3−x)) = 9 (6/(2x)) = ((10)/(8 )) ⇒ x = ((24)/(10)) x = ((12)/5)

$$\frac{\sqrt{\mathrm{3}+{x}}+\sqrt{\mathrm{3}−{x}}+\sqrt{\mathrm{3}+{x}}−\sqrt{\mathrm{3}−{x}}}{\:\sqrt{\mathrm{3}+{x}}+\sqrt{\mathrm{3}−{x}}−\sqrt{\mathrm{3}+{x}}+\sqrt{\mathrm{3}−{x}}}\:=\:\frac{\mathrm{2}+\mathrm{1}}{\mathrm{2}−\mathrm{1}} \\ $$$$\:\:\frac{\sqrt{\mathrm{3}+{x}}}{\:\sqrt{\mathrm{3}−{x}}}\:=\:\mathrm{3} \\ $$$$\:\:\frac{\mathrm{3}+{x}}{\mathrm{3}−{x}}\:=\:\mathrm{9} \\ $$$$\:\:\:\frac{\mathrm{6}}{\mathrm{2}{x}}\:=\:\frac{\mathrm{10}}{\mathrm{8}\:}\:\:\Rightarrow\:{x}\:=\:\frac{\mathrm{24}}{\mathrm{10}} \\ $$$$\:\:{x}\:\:\:=\:\:\frac{\mathrm{12}}{\mathrm{5}} \\ $$

Answered by puissant last updated on 24/Jul/22

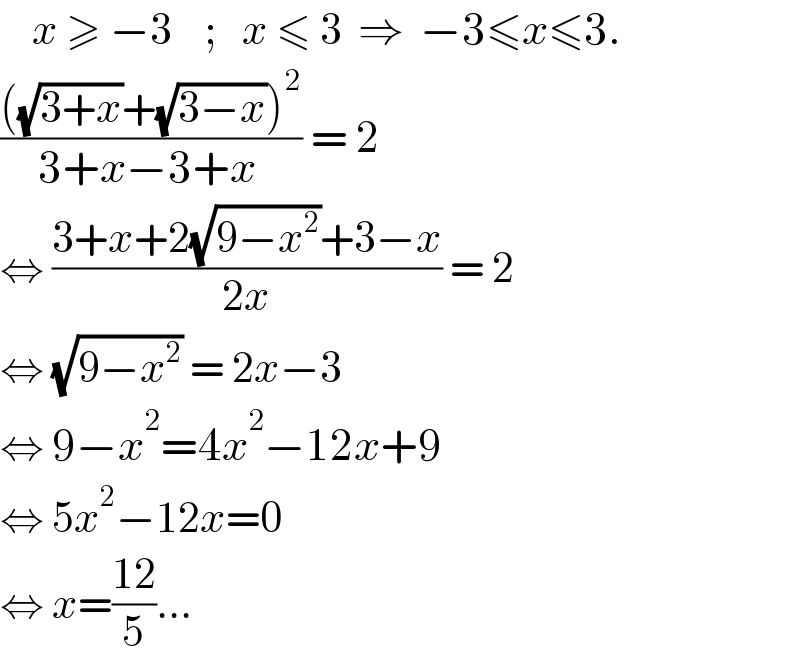
x ≥ −3 ; x ≤ 3 ⇒ −3≤x≤3. ((((√(3+x))+(√(3−x)))^2 )/(3+x−3+x )) = 2 ⇔ ((3+x+2(√(9−x^2 ))+3−x)/(2x)) = 2 ⇔ (√(9−x^2 )) = 2x−3 ⇔ 9−x^2 =4x^2 −12x+9 ⇔ 5x^2 −12x=0 ⇔ x=((12)/5)...

$$\:\:\:\:{x}\:\geqslant\:−\mathrm{3}\:\:\:\:;\:\:\:{x}\:\leqslant\:\mathrm{3}\:\:\Rightarrow\:\:−\mathrm{3}\leqslant{x}\leqslant\mathrm{3}. \\ $$$$\frac{\left(\sqrt{\mathrm{3}+{x}}+\sqrt{\mathrm{3}−{x}}\right)^{\mathrm{2}} }{\mathrm{3}+{x}−\mathrm{3}+{x}\:}\:=\:\mathrm{2} \\ $$$$\Leftrightarrow\:\frac{\mathrm{3}+{x}+\mathrm{2}\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }+\mathrm{3}−{x}}{\mathrm{2}{x}}\:=\:\mathrm{2} \\ $$$$\Leftrightarrow\:\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }\:=\:\mathrm{2}{x}−\mathrm{3} \\ $$$$\Leftrightarrow\:\mathrm{9}−{x}^{\mathrm{2}} =\mathrm{4}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{9} \\ $$$$\Leftrightarrow\:\mathrm{5}{x}^{\mathrm{2}} −\mathrm{12}{x}=\mathrm{0} \\ $$$$\Leftrightarrow\:{x}=\frac{\mathrm{12}}{\mathrm{5}}… \\ $$

Commented by som(math1967) last updated on 24/Jul/22

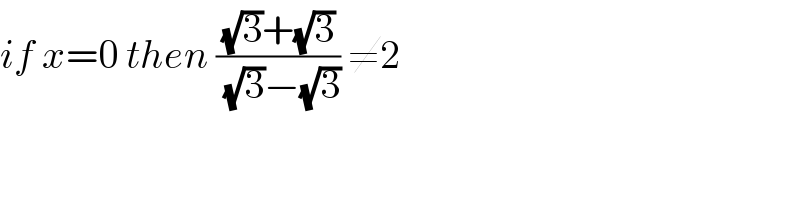
if x=0 then (((√3)+(√3))/( (√3)−(√3))) ≠2

$${if}\:{x}=\mathrm{0}\:{then}\:\frac{\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}}−\sqrt{\mathrm{3}}}\:\neq\mathrm{2} \\ $$

Answered by Rasheed.Sindhi last updated on 24/Jul/22

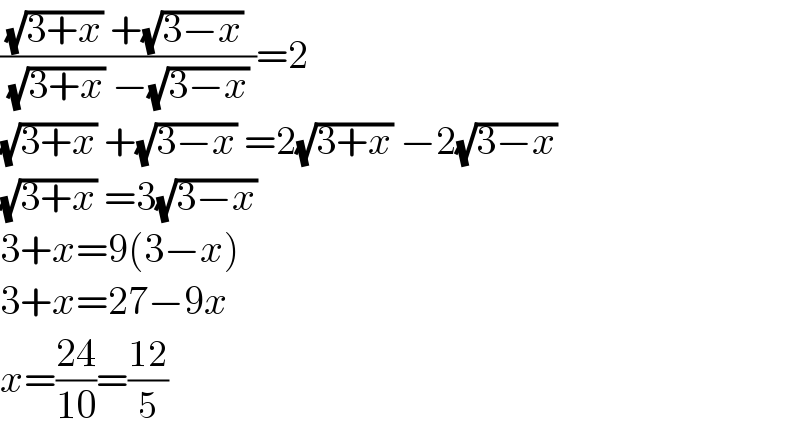
(((√(3+x)) +(√(3−x)) )/( (√(3+x)) −(√(3−x)) ))=2 (√(3+x)) +(√(3−x)) =2(√(3+x)) −2(√(3−x)) (√(3+x)) =3(√(3−x)) 3+x=9(3−x) 3+x=27−9x x=((24)/(10))=((12)/5)

$$\frac{\sqrt{\mathrm{3}+{x}}\:+\sqrt{\mathrm{3}−{x}}\:}{\:\sqrt{\mathrm{3}+{x}}\:−\sqrt{\mathrm{3}−{x}}\:}=\mathrm{2} \\ $$$$\sqrt{\mathrm{3}+{x}}\:+\sqrt{\mathrm{3}−{x}}\:=\mathrm{2}\sqrt{\mathrm{3}+{x}}\:−\mathrm{2}\sqrt{\mathrm{3}−{x}}\: \\ $$$$\sqrt{\mathrm{3}+{x}}\:=\mathrm{3}\sqrt{\mathrm{3}−{x}} \\ $$$$\mathrm{3}+{x}=\mathrm{9}\left(\mathrm{3}−{x}\right) \\ $$$$\mathrm{3}+{x}=\mathrm{27}−\mathrm{9}{x} \\ $$$${x}=\frac{\mathrm{24}}{\mathrm{10}}=\frac{\mathrm{12}}{\mathrm{5}} \\ $$

Commented by AgniMath last updated on 25/Jul/22

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{the}\:\mathrm{easiest}\:\mathrm{solution} \\ $$

Commented by Rasheed.Sindhi last updated on 26/Jul/22

��

Facebook Tweet Pin

Leave a Reply Cancel reply