Question-174153

Question Number 174153 by daus last updated on 26/Jul/22

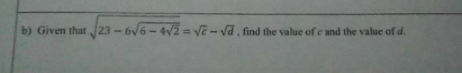
Commented by mr W last updated on 26/Jul/22

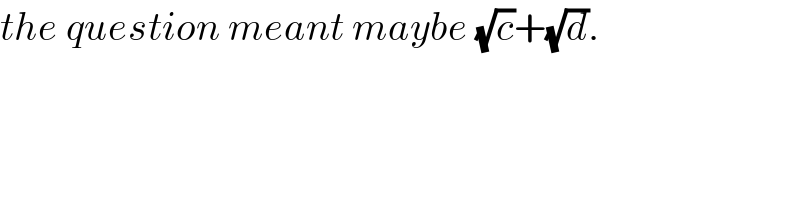
$${the}\:{question}\:{meant}\:{maybe}\:\sqrt{{c}}+\sqrt{{d}}. \\ $$

Answered by mr W last updated on 26/Jul/22

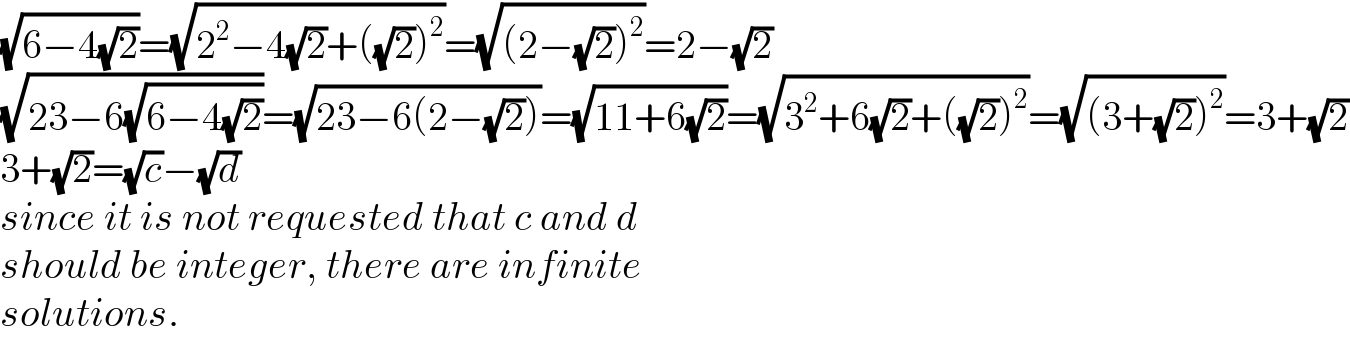
(√(6−4(√2)))=(√(2^2 −4(√2)+((√2))^2 ))=(√((2−(√2))^2 ))=2−(√2) (√(23−6(√(6−4(√2)))))=(√(23−6(2−(√2))))=(√(11+6(√2)))=(√(3^2 +6(√2)+((√2))^2 ))=(√((3+(√2))^2 ))=3+(√2) 3+(√2)=(√c)−(√d) since it is not requested that c and d should be integer, there are infinite solutions.

$$\sqrt{\mathrm{6}−\mathrm{4}\sqrt{\mathrm{2}}}=\sqrt{\mathrm{2}^{\mathrm{2}} −\mathrm{4}\sqrt{\mathrm{2}}+\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }=\sqrt{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }=\mathrm{2}−\sqrt{\mathrm{2}} \\ $$$$\sqrt{\mathrm{23}−\mathrm{6}\sqrt{\mathrm{6}−\mathrm{4}\sqrt{\mathrm{2}}}}=\sqrt{\mathrm{23}−\mathrm{6}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)}=\sqrt{\mathrm{11}+\mathrm{6}\sqrt{\mathrm{2}}}=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{6}\sqrt{\mathrm{2}}+\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }=\sqrt{\left(\mathrm{3}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }=\mathrm{3}+\sqrt{\mathrm{2}} \\ $$$$\mathrm{3}+\sqrt{\mathrm{2}}=\sqrt{{c}}−\sqrt{{d}} \\ $$$${since}\:{it}\:{is}\:{not}\:{requested}\:{that}\:{c}\:{and}\:{d} \\ $$$${should}\:{be}\:{integer},\:{there}\:{are}\:{infinite} \\ $$$${solutions}. \\ $$

Answered by BaliramKumar last updated on 26/Jul/22

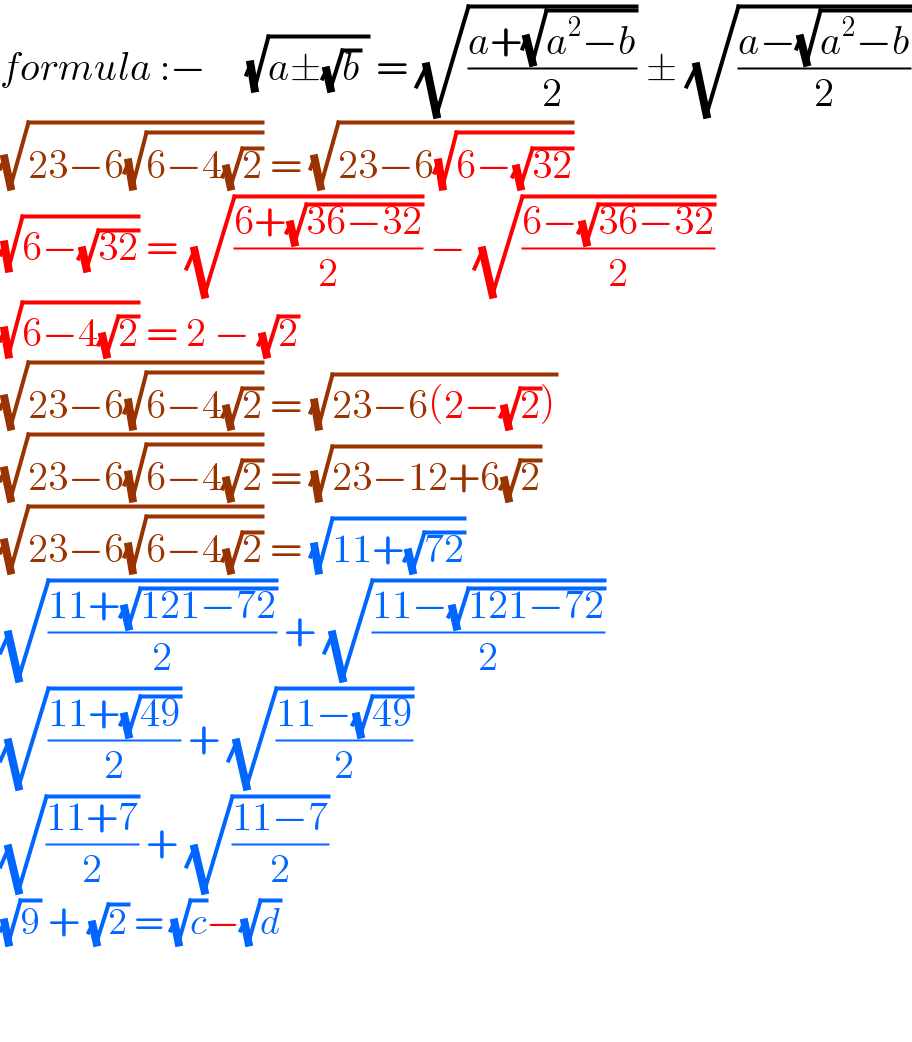
formula :− (√(a±(√b) )) = (√((a+(√(a^2 −b)))/2)) ± (√((a−(√(a^2 −b)))/2)) (√(23−6(√(6−4(√2))))) = (√(23−6(√(6−(√(32)))))) (√(6−(√(32)))) = (√((6+(√(36−32)))/2)) − (√((6−(√(36−32)))/2)) (√(6−4(√2))) = 2 − (√2) (√(23−6(√(6−4(√2))))) = (√(23−6(2−(√2)))) (√(23−6(√(6−4(√2))))) = (√(23−12+6(√2))) (√(23−6(√(6−4(√2))))) = (√(11+(√(72)))) (√((11+(√(121−72)))/2)) + (√((11−(√(121−72)))/2)) (√((11+(√(49)))/2)) + (√((11−(√(49)))/2)) (√((11+7)/2)) + (√((11−7)/2)) (√9) + (√2) = (√c)−(√d)

$${formula}\::−\:\:\:\:\:\sqrt{{a}\pm\sqrt{{b}}\:}\:=\:\sqrt{\frac{{a}+\sqrt{{a}^{\mathrm{2}} −{b}}}{\mathrm{2}}}\:\pm\:\sqrt{\frac{{a}−\sqrt{{a}^{\mathrm{2}} −{b}}}{\mathrm{2}}} \\ $$$$\sqrt{\mathrm{23}−\mathrm{6}\sqrt{\mathrm{6}−\mathrm{4}\sqrt{\mathrm{2}}}}\:=\:\sqrt{\mathrm{23}−\mathrm{6}\sqrt{\mathrm{6}−\sqrt{\mathrm{32}}}} \\ $$$$\sqrt{\mathrm{6}−\sqrt{\mathrm{32}}}\:=\:\sqrt{\frac{\mathrm{6}+\sqrt{\mathrm{36}−\mathrm{32}}}{\mathrm{2}}}\:−\:\sqrt{\frac{\mathrm{6}−\sqrt{\mathrm{36}−\mathrm{32}}}{\mathrm{2}}} \\ $$$$\sqrt{\mathrm{6}−\mathrm{4}\sqrt{\mathrm{2}}}\:=\:\mathrm{2}\:−\:\sqrt{\mathrm{2}} \\ $$$$\sqrt{\mathrm{23}−\mathrm{6}\sqrt{\mathrm{6}−\mathrm{4}\sqrt{\mathrm{2}}}}\:=\:\sqrt{\mathrm{23}−\mathrm{6}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)} \\ $$$$\sqrt{\mathrm{23}−\mathrm{6}\sqrt{\mathrm{6}−\mathrm{4}\sqrt{\mathrm{2}}}}\:=\:\sqrt{\mathrm{23}−\mathrm{12}+\mathrm{6}\sqrt{\mathrm{2}}} \\ $$$$\sqrt{\mathrm{23}−\mathrm{6}\sqrt{\mathrm{6}−\mathrm{4}\sqrt{\mathrm{2}}}}\:=\:\sqrt{\mathrm{11}+\sqrt{\mathrm{72}}} \\ $$$$\sqrt{\frac{\mathrm{11}+\sqrt{\mathrm{121}−\mathrm{72}}}{\mathrm{2}}}\:+\:\sqrt{\frac{\mathrm{11}−\sqrt{\mathrm{121}−\mathrm{72}}}{\mathrm{2}}} \\ $$$$\sqrt{\frac{\mathrm{11}+\sqrt{\mathrm{49}}}{\mathrm{2}}}\:+\:\sqrt{\frac{\mathrm{11}−\sqrt{\mathrm{49}}}{\mathrm{2}}} \\ $$$$\sqrt{\frac{\mathrm{11}+\mathrm{7}}{\mathrm{2}}}\:+\:\sqrt{\frac{\mathrm{11}−\mathrm{7}}{\mathrm{2}}} \\ $$$$\sqrt{\mathrm{9}}\:+\:\sqrt{\mathrm{2}}\:=\:\sqrt{{c}}−\sqrt{{d}} \\ $$$$ \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply