Question Number 174194 by mokys last updated on 26/Jul/22
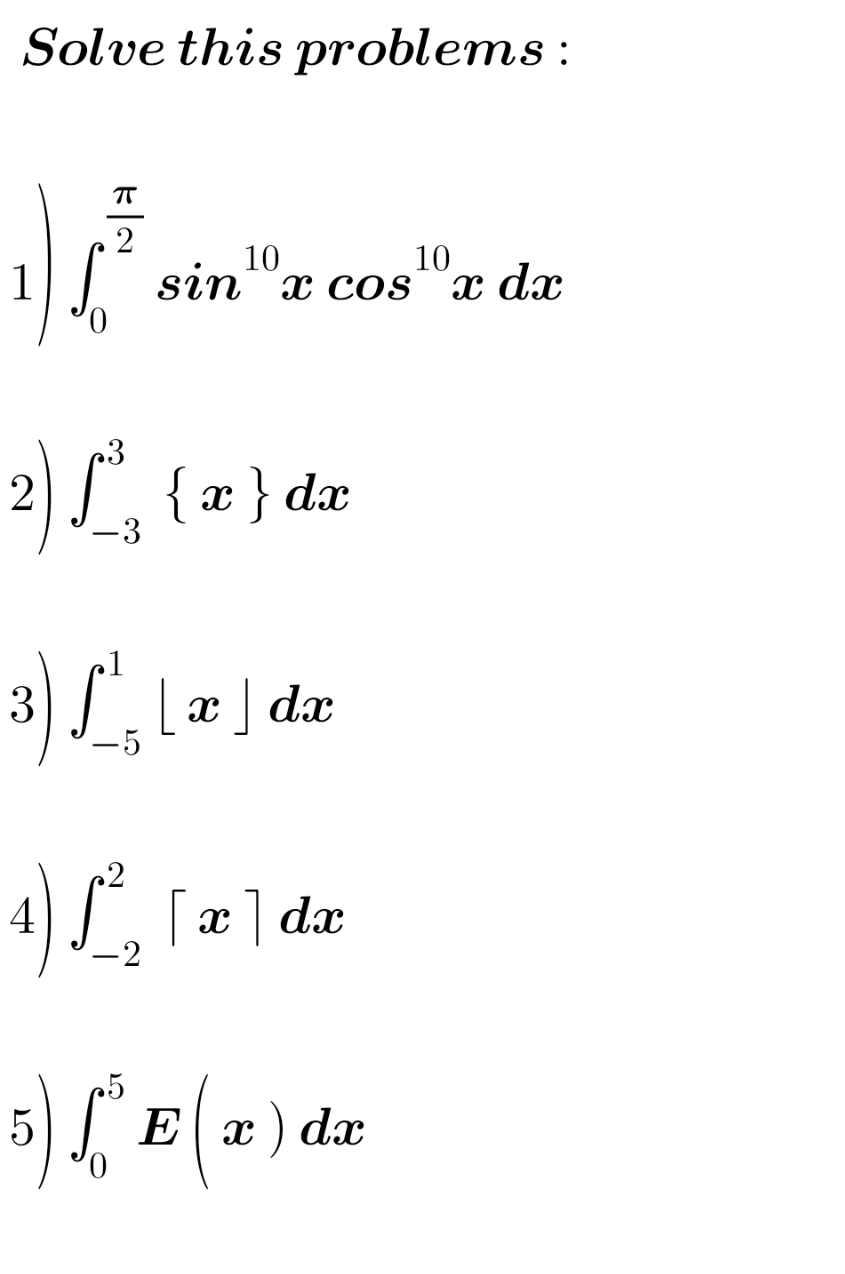
Answered by Mathspace last updated on 27/Jul/22
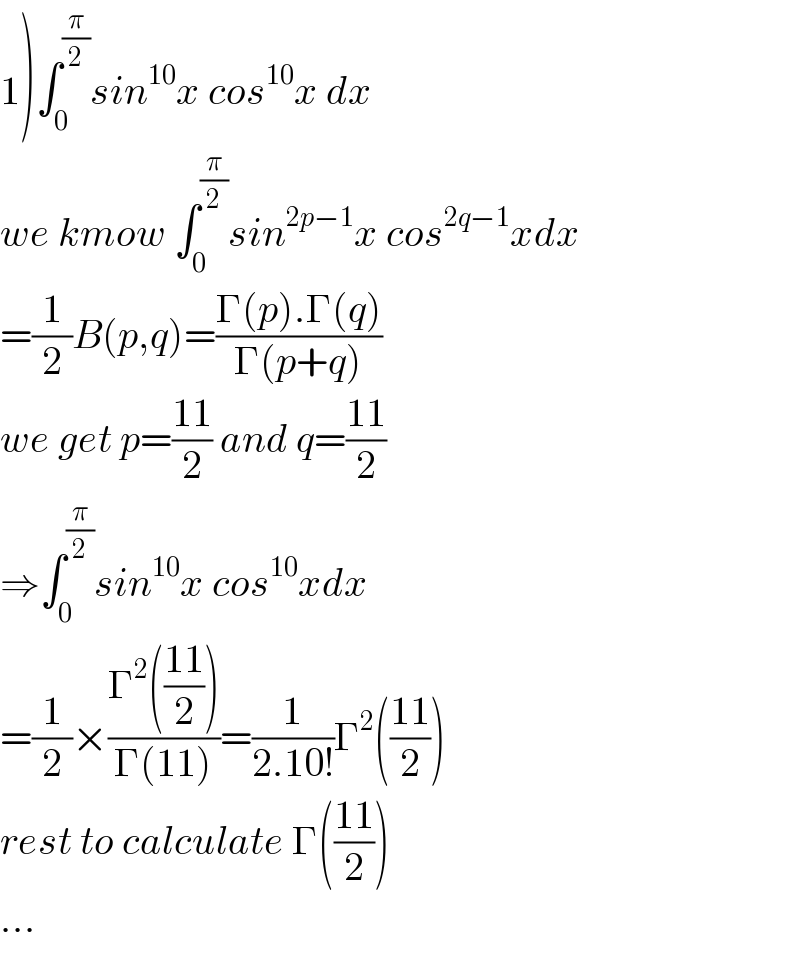
$$\left.\mathrm{1}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{10}} {x}\:{cos}^{\mathrm{10}} {x}\:{dx} \\ $$$${we}\:{kmow}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}{p}−\mathrm{1}} {x}\:{cos}^{\mathrm{2}{q}−\mathrm{1}} {xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{B}\left({p},{q}\right)=\frac{\Gamma\left({p}\right).\Gamma\left({q}\right)}{\Gamma\left({p}+{q}\right)} \\ $$$${we}\:{get}\:{p}=\frac{\mathrm{11}}{\mathrm{2}}\:{and}\:{q}=\frac{\mathrm{11}}{\mathrm{2}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{10}} {x}\:{cos}^{\mathrm{10}} {xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{11}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{11}\right)}=\frac{\mathrm{1}}{\mathrm{2}.\mathrm{10}!}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{11}}{\mathrm{2}}\right) \\ $$$${rest}\:{to}\:{calculate}\:\Gamma\left(\frac{\mathrm{11}}{\mathrm{2}}\right) \\ $$$$… \\ $$
Commented by aleks041103 last updated on 27/Jul/22

$${I}\left({p},{q}\right)=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {sin}^{\mathrm{2}{p}−\mathrm{1}} {x}\:{cos}^{\mathrm{2}{q}−\mathrm{1}} {x}\:{dx} \\ $$$${t}={sin}^{\mathrm{2}} {x} \\ $$$${dt}=\mathrm{2}{sinx}\:{cosx}\:{dx} \\ $$$${I}\left({p},{q}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \left({sin}^{\mathrm{2}} {x}\right)^{{p}−\mathrm{1}} \:\left({cos}^{\mathrm{2}} {x}\right)^{{q}−\mathrm{1}} \left(\mathrm{2}{sinx}\:{cosx}\:{dx}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} {t}^{{p}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{q}−\mathrm{1}} {dt}=\frac{\mathrm{1}}{\mathrm{2}}{B}\left({p},{q}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {sin}^{\alpha} {x}\:{cos}^{\beta} {x}\:{dx}=\frac{\mathrm{1}}{\mathrm{2}}{B}\left(\frac{\mathrm{1}+\alpha}{\mathrm{2}},\frac{\mathrm{1}+\beta}{\mathrm{2}}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {sin}^{\alpha} {x}\:{cos}^{\beta} {x}\:{dx}=\frac{\Gamma\left(\frac{\mathrm{1}+\alpha}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}+\beta}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\mathrm{1}+\frac{\alpha+\beta}{\mathrm{2}}\right)} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {sin}^{\mathrm{10}} {x}\:{cos}^{\mathrm{10}} {x}\:{dx}=\frac{\Gamma\left(\frac{\mathrm{11}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}\Gamma\left(\mathrm{11}\right)}=\frac{\left(\left(\mathrm{9}/\mathrm{2}\right)!\right)^{\mathrm{2}} }{\mathrm{2}.\mathrm{10}!} \\ $$$$\left(\frac{\mathrm{9}}{\mathrm{2}}\right)!=\frac{\mathrm{9}}{\mathrm{2}}\:\left(\frac{\mathrm{7}}{\mathrm{2}}\right)!=…=\frac{\mathrm{9}.\mathrm{7}.\mathrm{5}.\mathrm{3}}{\mathrm{2}.\mathrm{2}.\mathrm{2}.\mathrm{2}}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)!=\frac{\mathrm{9}.\mathrm{7}.\mathrm{5}.\mathrm{3}}{\mathrm{32}}\sqrt{\pi} \\ $$$$\Rightarrow\left(\left(\mathrm{9}/\mathrm{2}\right)!\right)^{\mathrm{2}} /\left(\mathrm{2}.\mathrm{10}!\right)=\frac{\mathrm{893025}}{\mathrm{2048}.\mathrm{3628800}}\pi=\frac{\mathrm{893025}}{\mathrm{7431782400}}\pi= \\ $$$$=\frac{\mathrm{35721}\pi}{\mathrm{297271296}}=\frac{\mathrm{441}\pi}{\mathrm{3670016}}=\frac{\mathrm{63}\pi}{\mathrm{524288}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {sin}^{\alpha} {x}\:{cos}^{\beta} {x}\:{dx}=\frac{\mathrm{63}\pi}{\mathrm{524288}} \\ $$$$ \\ $$$$ \\ $$
Answered by Mathspace last updated on 27/Jul/22
![3)∫_(−5) ^1 [x]dx =_(x=−5+t) ∫_0 ^6 [t−5]dt =∫_0 ^6 ([t]−5)dt =∫_0 ^6 [t]dt−30 =Σ_(k=0) ^5 ∫_k ^(k+1) kdt−30 =Σ_(k=0) ^5 k −30 =((5.6)/2)−30 =15−30=−15](https://www.tinkutara.com/question/Q174206.png)
$$\left.\mathrm{3}\right)\int_{−\mathrm{5}} ^{\mathrm{1}} \left[{x}\right]{dx}\:=_{{x}=−\mathrm{5}+{t}} \:\int_{\mathrm{0}} ^{\mathrm{6}} \left[{t}−\mathrm{5}\right]{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{6}} \left(\left[{t}\right]−\mathrm{5}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{6}} \left[{t}\right]{dt}−\mathrm{30} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \int_{{k}} ^{{k}+\mathrm{1}} {kdt}−\mathrm{30} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} {k}\:−\mathrm{30} \\ $$$$=\frac{\mathrm{5}.\mathrm{6}}{\mathrm{2}}−\mathrm{30}\:=\mathrm{15}−\mathrm{30}=−\mathrm{15} \\ $$
Answered by Mathspace last updated on 27/Jul/22
![4) ∫_(−2) ^2 [x]dx=_(x=−2+t) ∫_0 ^4 [−2+t]dt =∫_0 ^4 (−2+[t])dt =−8+∫_0 ^4 [t]dt =−8+Σ_(k=0) ^3 ∫_k ^(k+1) kdt =−8+Σ_(k=1) ^3 k =−8+((3.4)/2)=−8+6=2](https://www.tinkutara.com/question/Q174207.png)
$$\left.\mathrm{4}\right)\:\int_{−\mathrm{2}} ^{\mathrm{2}} \left[{x}\right]{dx}=_{{x}=−\mathrm{2}+{t}} \:\int_{\mathrm{0}} ^{\mathrm{4}} \left[−\mathrm{2}+{t}\right]{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{4}} \left(−\mathrm{2}+\left[{t}\right]\right){dt} \\ $$$$=−\mathrm{8}+\int_{\mathrm{0}} ^{\mathrm{4}} \left[{t}\right]{dt} \\ $$$$=−\mathrm{8}+\sum_{{k}=\mathrm{0}} ^{\mathrm{3}} \int_{{k}} ^{{k}+\mathrm{1}} {kdt} \\ $$$$=−\mathrm{8}+\sum_{{k}=\mathrm{1}} ^{\mathrm{3}} {k} \\ $$$$=−\mathrm{8}+\frac{\mathrm{3}.\mathrm{4}}{\mathrm{2}}=−\mathrm{8}+\mathrm{6}=\mathrm{2} \\ $$
Answered by Mathspace last updated on 27/Jul/22
![2)∫_(−3) ^3 {x}dx=∫_(−3) ^3 (x−[x])dx =∫_(−3) ^3 xdx(→0)−∫_(−3) ^3 [x]dx =_(x=−3+t) −∫_o ^6 (−3+[t])dt =18−Σ_(k=0) ^5 ∫_k ^(k+1) kdt =18−Σ_(k=1) ^5 k =18−((5.6)/2)=18−15=3](https://www.tinkutara.com/question/Q174208.png)
$$\left.\mathrm{2}\right)\int_{−\mathrm{3}} ^{\mathrm{3}} \left\{{x}\right\}{dx}=\int_{−\mathrm{3}} ^{\mathrm{3}} \left({x}−\left[{x}\right]\right){dx} \\ $$$$=\int_{−\mathrm{3}} ^{\mathrm{3}} {xdx}\left(\rightarrow\mathrm{0}\right)−\int_{−\mathrm{3}} ^{\mathrm{3}} \left[{x}\right]{dx} \\ $$$$=_{{x}=−\mathrm{3}+{t}} \:\:−\int_{{o}} ^{\mathrm{6}} \left(−\mathrm{3}+\left[{t}\right]\right){dt} \\ $$$$=\mathrm{18}−\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \int_{{k}} ^{{k}+\mathrm{1}} {kdt} \\ $$$$=\mathrm{18}−\sum_{{k}=\mathrm{1}} ^{\mathrm{5}} {k} \\ $$$$=\mathrm{18}−\frac{\mathrm{5}.\mathrm{6}}{\mathrm{2}}=\mathrm{18}−\mathrm{15}=\mathrm{3} \\ $$
