Question Number 174253 by mathlove last updated on 28/Jul/22

Answered by mnjuly1970 last updated on 28/Jul/22
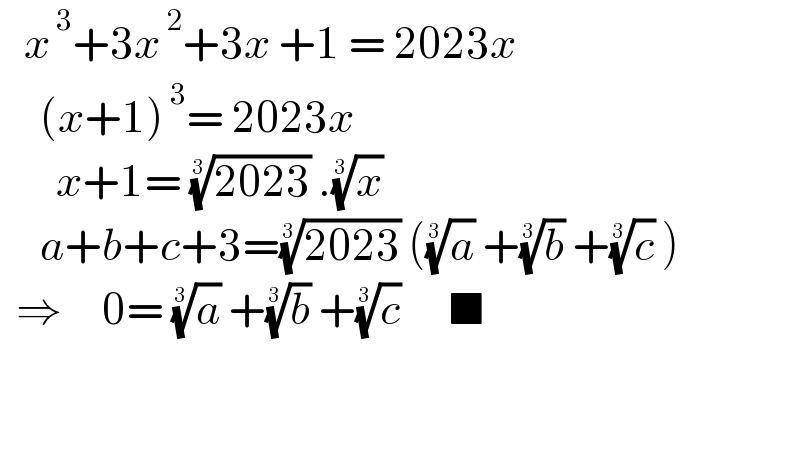
$$\:\:\:{x}^{\:\mathrm{3}} +\mathrm{3}{x}^{\:\mathrm{2}} +\mathrm{3}{x}\:+\mathrm{1}\:=\:\mathrm{2023}{x} \\ $$$$\:\:\:\:\:\left({x}+\mathrm{1}\right)^{\:\mathrm{3}} =\:\mathrm{2023}{x} \\ $$$$\:\:\:\:\:\:\:{x}+\mathrm{1}=\:\sqrt[{\mathrm{3}}]{\mathrm{2023}}\:.\sqrt[{\mathrm{3}}]{{x}} \\ $$$$\:\:\:\:\:{a}+{b}+{c}+\mathrm{3}=\sqrt[{\mathrm{3}}]{\mathrm{2023}}\:\left(\sqrt[{\mathrm{3}}]{{a}}\:+\sqrt[{\mathrm{3}}]{{b}}\:+\sqrt[{\mathrm{3}}]{{c}}\:\right) \\ $$$$\:\:\Rightarrow\:\:\:\:\:\mathrm{0}=\:\sqrt[{\mathrm{3}}]{{a}}\:+\sqrt[{\mathrm{3}}]{{b}}\:+\sqrt[{\mathrm{3}}]{{c}}\:\:\:\:\:\:\blacksquare \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\: \\ $$
Commented by Rasheed.Sindhi last updated on 28/Jul/22

$$\mathrm{e}^{\mathrm{x}} \mathrm{cellent}\:\mathrm{sir}! \\ $$
Commented by mnjuly1970 last updated on 28/Jul/22
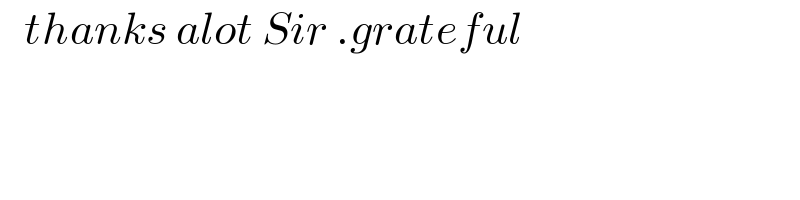
$$\:\:\:{thanks}\:{alot}\:{Sir}\:.{grateful} \\ $$
Commented by mathlove last updated on 28/Jul/22

$${thanks} \\ $$
