Question-174276

Question Number 174276 by cortano1 last updated on 28/Jul/22

Answered by blackmamba last updated on 28/Jul/22

lim_(x→0) ((1−((cos (2021x)))^(1/(2022)) )/x^2 ) = lim_(x→0) ((1−((1−2sin^2 (((2021x)/2))))^(1/(2022)) )/x^2 ) = lim_(x→0) ((1−(1−((2sin^2 (((2021x)/2)))/(2022))))/x^2 ) = (1/(1011)) ×lim_(x→0) [((sin (((2021x)/2)))/x) ]^2 = (1/(1011))×(((2021)^2 )/4) = ((2021^2 )/(4044))

$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\sqrt[{\mathrm{2022}}]{\mathrm{cos}\:\left(\mathrm{2021}{x}\right)}}{{x}^{\mathrm{2}} }\:= \\ $$$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\sqrt[{\mathrm{2022}}]{\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{2021}{x}}{\mathrm{2}}\right)}}{{x}^{\mathrm{2}} } \\ $$$$\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{2021}{x}}{\mathrm{2}}\right)}{\mathrm{2022}}\right)}{{x}^{\mathrm{2}} } \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{1011}}\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\frac{\mathrm{sin}\:\left(\frac{\mathrm{2021}{x}}{\mathrm{2}}\right)}{{x}}\:\right]^{\mathrm{2}} \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{1011}}×\frac{\left(\mathrm{2021}\right)^{\mathrm{2}} }{\mathrm{4}}\:=\:\frac{\mathrm{2021}^{\mathrm{2}} }{\mathrm{4044}} \\ $$

Answered by Mathspace last updated on 28/Jul/22

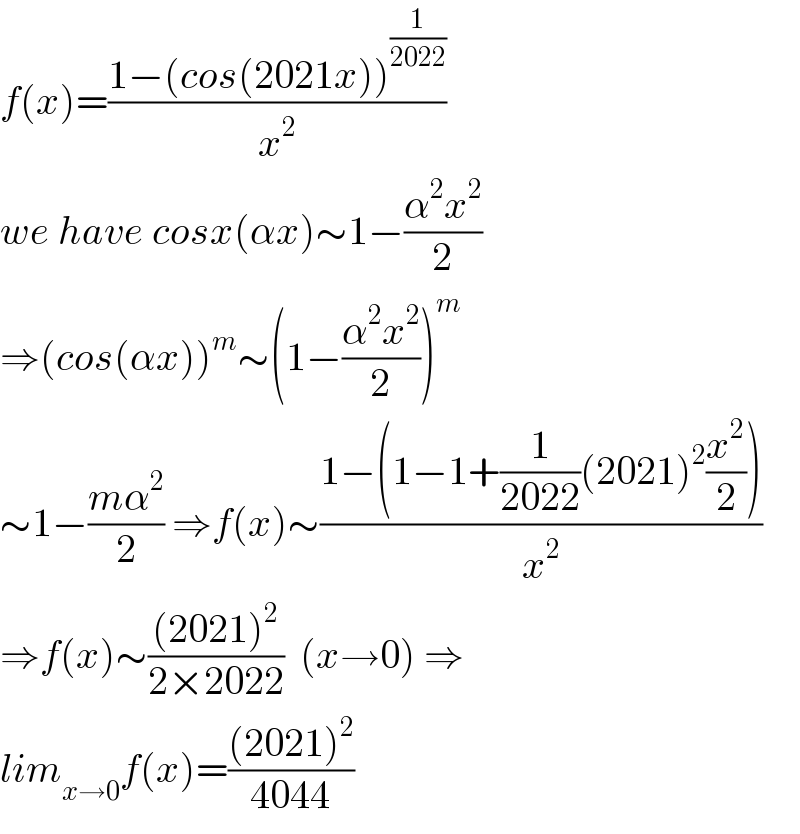
f(x)=((1−(cos(2021x))^(1/(2022)) )/x^2 ) we have cosx(αx)∼1−((α^2 x^2 )/2) ⇒(cos(αx))^m ∼(1−((α^2 x^2 )/2))^m ∼1−((mα^2 )/2) ⇒f(x)∼((1−(1−1+(1/(2022))(2021)^2 (x^2 /2)))/x^2 ) ⇒f(x)∼(((2021)^2 )/(2×2022)) (x→0) ⇒ lim_(x→0) f(x)=(((2021)^2 )/(4044))

$${f}\left({x}\right)=\frac{\mathrm{1}−\left({cos}\left(\mathrm{2021}{x}\right)\right)^{\frac{\mathrm{1}}{\mathrm{2022}}} }{{x}^{\mathrm{2}} } \\ $$$${we}\:{have}\:{cosx}\left(\alpha{x}\right)\sim\mathrm{1}−\frac{\alpha^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\left({cos}\left(\alpha{x}\right)\right)^{{m}} \sim\left(\mathrm{1}−\frac{\alpha^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}}\right)^{{m}} \\ $$$$\sim\mathrm{1}−\frac{{m}\alpha^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow{f}\left({x}\right)\sim\frac{\mathrm{1}−\left(\mathrm{1}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2022}}\left(\mathrm{2021}\right)^{\mathrm{2}} \frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{f}\left({x}\right)\sim\frac{\left(\mathrm{2021}\right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{2022}}\:\:\left({x}\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)=\frac{\left(\mathrm{2021}\right)^{\mathrm{2}} }{\mathrm{4044}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply