Question Number 174283 by ajfour last updated on 28/Jul/22
Commented by ajfour last updated on 28/Jul/22
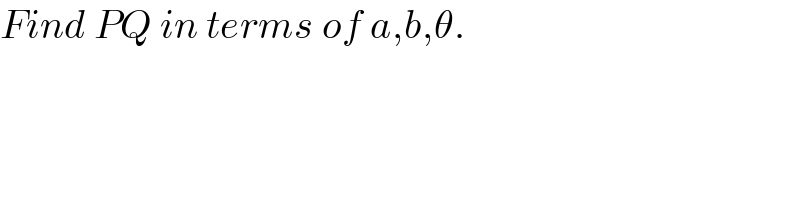
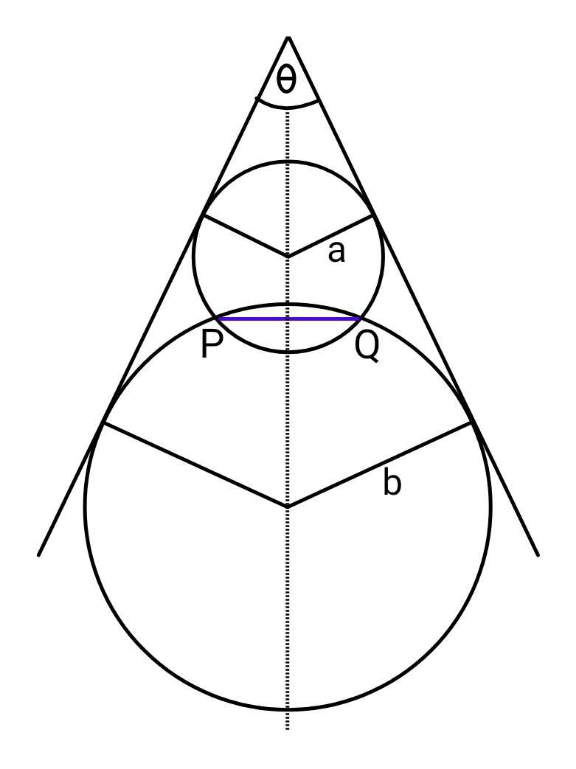
$${Find}\:{PQ}\:{in}\:{terms}\:{of}\:{a},{b},\theta. \\ $$
Answered by mr W last updated on 29/Jul/22
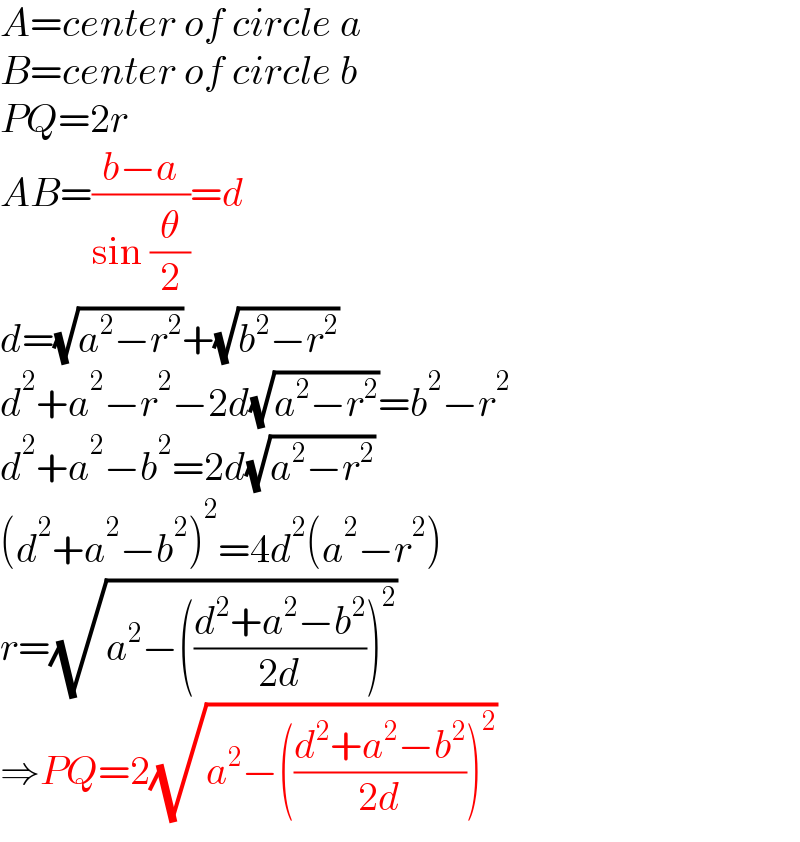
$${A}={center}\:{of}\:{circle}\:{a} \\ $$$${B}={center}\:{of}\:{circle}\:{b} \\ $$$${PQ}=\mathrm{2}{r} \\ $$$${AB}=\frac{{b}−{a}}{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}={d} \\ $$$${d}=\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$${d}^{\mathrm{2}} +{a}^{\mathrm{2}} −{r}^{\mathrm{2}} −\mathrm{2}{d}\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }={b}^{\mathrm{2}} −{r}^{\mathrm{2}} \\ $$$${d}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{2}{d}\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\left({d}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}{d}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{r}^{\mathrm{2}} \right) \\ $$$${r}=\sqrt{{a}^{\mathrm{2}} −\left(\frac{{d}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{d}}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{PQ}=\mathrm{2}\sqrt{{a}^{\mathrm{2}} −\left(\frac{{d}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{d}}\right)^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 29/Jul/22
$${wonderful},\:{thanks}\:{Sir}! \\ $$
Commented by Tawa11 last updated on 29/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
