Question Number 174287 by Engr_Jidda last updated on 28/Jul/22

Answered by haf last updated on 28/Jul/22

$${use}\:\:{ln}\:{function} \\ $$
Commented by Engr_Jidda last updated on 29/Jul/22

$${pls}\:{help}\:{me}\:{out} \\ $$
Answered by Rasheed.Sindhi last updated on 29/Jul/22
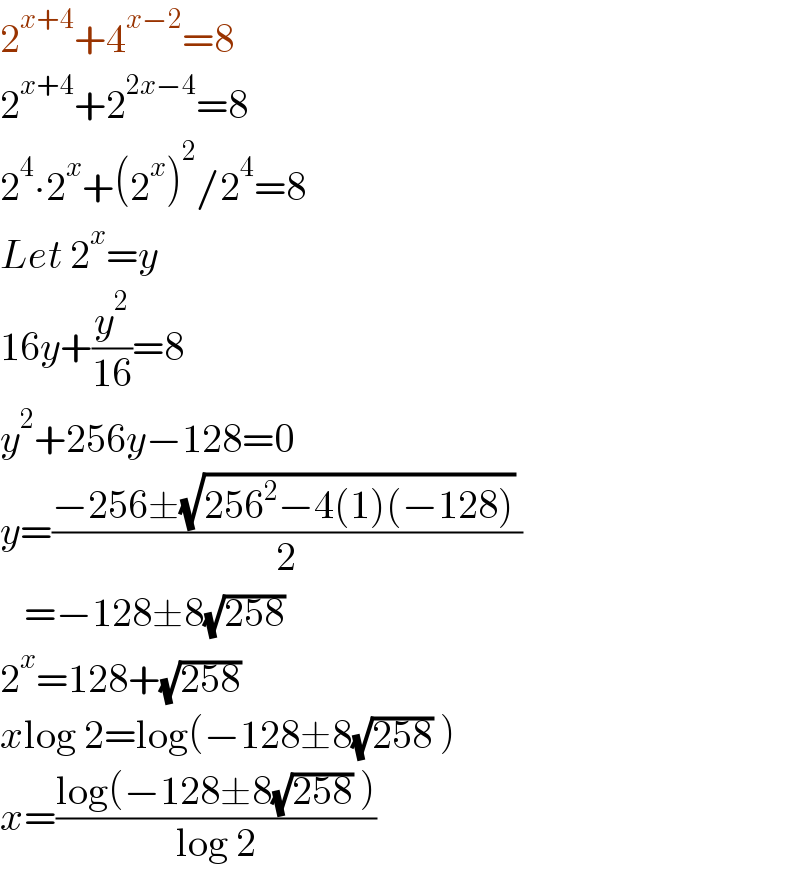
$$\mathrm{2}^{{x}+\mathrm{4}} +\mathrm{4}^{{x}−\mathrm{2}} =\mathrm{8} \\ $$$$\mathrm{2}^{{x}+\mathrm{4}} +\mathrm{2}^{\mathrm{2}{x}−\mathrm{4}} =\mathrm{8} \\ $$$$\mathrm{2}^{\mathrm{4}} \centerdot\mathrm{2}^{{x}} +\left(\mathrm{2}^{{x}} \right)^{\mathrm{2}} /\mathrm{2}^{\mathrm{4}} =\mathrm{8} \\ $$$${Let}\:\mathrm{2}^{{x}} ={y} \\ $$$$\mathrm{16}{y}+\frac{{y}^{\mathrm{2}} }{\mathrm{16}}=\mathrm{8} \\ $$$${y}^{\mathrm{2}} +\mathrm{256}{y}−\mathrm{128}=\mathrm{0} \\ $$$${y}=\frac{−\mathrm{256}\pm\sqrt{\mathrm{256}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(−\mathrm{128}\right)}\:}{\mathrm{2}} \\ $$$$\:\:\:=−\mathrm{128}\pm\mathrm{8}\sqrt{\mathrm{258}} \\ $$$$\mathrm{2}^{{x}} =\mathrm{128}+\sqrt{\mathrm{258}} \\ $$$${x}\mathrm{log}\:\mathrm{2}=\mathrm{log}\left(−\mathrm{128}\pm\mathrm{8}\sqrt{\mathrm{258}}\:\right) \\ $$$${x}=\frac{\mathrm{log}\left(−\mathrm{128}\pm\mathrm{8}\sqrt{\mathrm{258}}\:\right)}{\mathrm{log}\:\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 31/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 31/Jul/22

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{miss}}! \\ $$
