Question Number 174304 by dragan91 last updated on 29/Jul/22

Answered by mr W last updated on 29/Jul/22
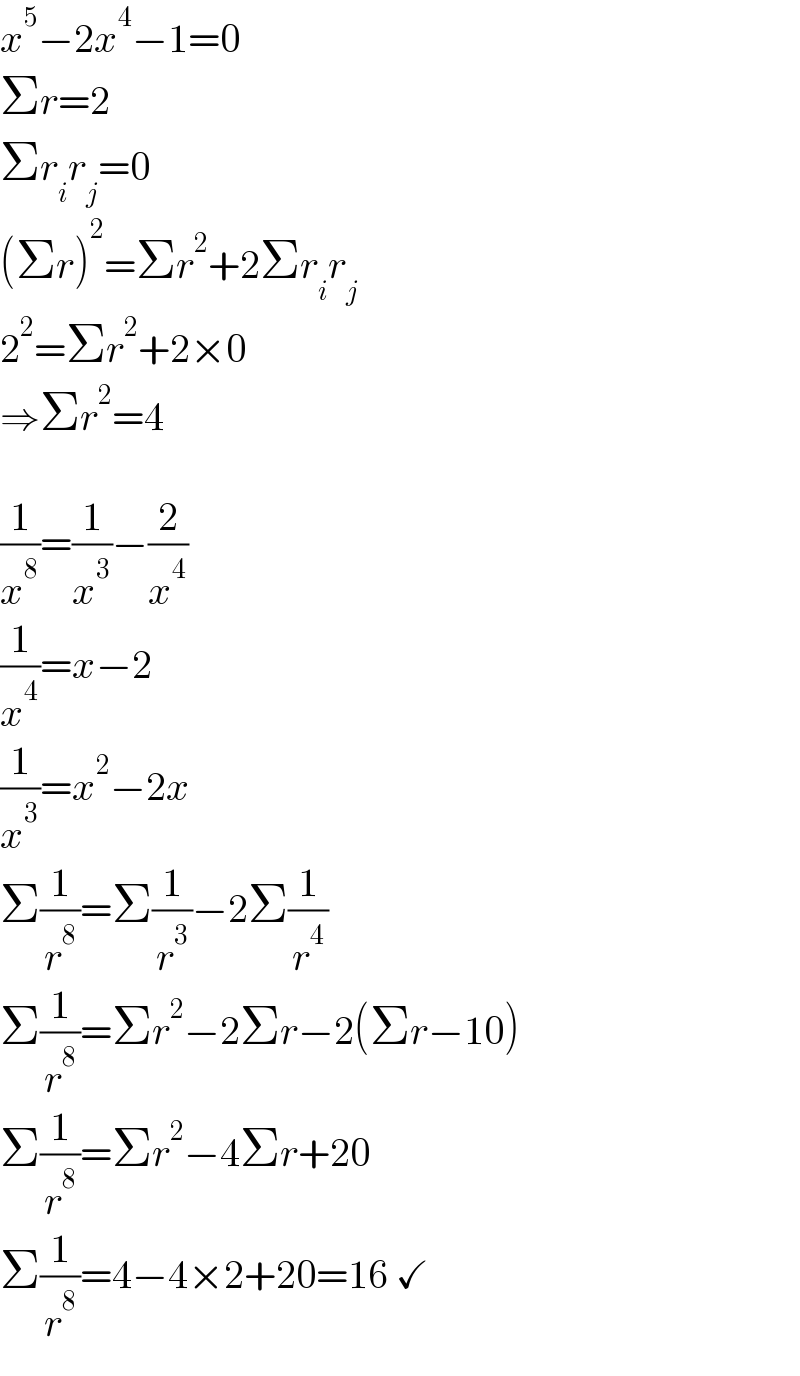
$${x}^{\mathrm{5}} −\mathrm{2}{x}^{\mathrm{4}} −\mathrm{1}=\mathrm{0} \\ $$$$\Sigma{r}=\mathrm{2} \\ $$$$\Sigma{r}_{{i}} {r}_{{j}} =\mathrm{0} \\ $$$$\left(\Sigma{r}\right)^{\mathrm{2}} =\Sigma{r}^{\mathrm{2}} +\mathrm{2}\Sigma{r}_{{i}} {r}_{{j}} \\ $$$$\mathrm{2}^{\mathrm{2}} =\Sigma{r}^{\mathrm{2}} +\mathrm{2}×\mathrm{0} \\ $$$$\Rightarrow\Sigma{r}^{\mathrm{2}} =\mathrm{4} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{8}} }=\frac{\mathrm{1}}{{x}^{\mathrm{3}} }−\frac{\mathrm{2}}{{x}^{\mathrm{4}} } \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{4}} }={x}−\mathrm{2} \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{3}} }={x}^{\mathrm{2}} −\mathrm{2}{x} \\ $$$$\Sigma\frac{\mathrm{1}}{{r}^{\mathrm{8}} }=\Sigma\frac{\mathrm{1}}{{r}^{\mathrm{3}} }−\mathrm{2}\Sigma\frac{\mathrm{1}}{{r}^{\mathrm{4}} } \\ $$$$\Sigma\frac{\mathrm{1}}{{r}^{\mathrm{8}} }=\Sigma{r}^{\mathrm{2}} −\mathrm{2}\Sigma{r}−\mathrm{2}\left(\Sigma{r}−\mathrm{10}\right) \\ $$$$\Sigma\frac{\mathrm{1}}{{r}^{\mathrm{8}} }=\Sigma{r}^{\mathrm{2}} −\mathrm{4}\Sigma{r}+\mathrm{20} \\ $$$$\Sigma\frac{\mathrm{1}}{{r}^{\mathrm{8}} }=\mathrm{4}−\mathrm{4}×\mathrm{2}+\mathrm{20}=\mathrm{16}\:\checkmark \\ $$
Commented by Tawa11 last updated on 29/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
