Question Number 174315 by mnjuly1970 last updated on 29/Jul/22
Answered by aleks041103 last updated on 29/Jul/22

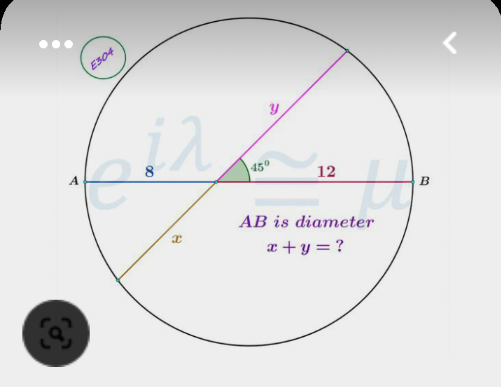
$${if}\:{the}\:{intersection}\:{point}\:{on}\:{AB}\:{is}\:{O}, \\ $$$${let}'{s}\:{set}\:{its}\:{coordinates}\:{to}\:\left(\mathrm{0},\mathrm{0}\right) \\ $$$${then}\:{OB}\:{is}\:{the}\:{x}\:{axis}. \\ $$$${then}\:{th}\:{equation}\:{of}\:{the}\:{slanted}\:{line}\:{is}: \\ $$$${y}={x} \\ $$$${and}\:{the}\:{eqn}.\:{of}\:{the}\:{circle}\:{is}: \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{100} \\ $$$${the}\:{intersection}\:{is} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} =\mathrm{100} \\ $$$$\Rightarrow\mathrm{2}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}=\mathrm{100} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}=\mathrm{50} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{48}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{6}{x}−\mathrm{48}=\mathrm{0} \\ $$$${x}\left({x}−\mathrm{8}\right)+\mathrm{6}\left({x}−\mathrm{8}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({x}+\mathrm{6}\right)\left({x}−\mathrm{8}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}_{{intersec}} =+\mathrm{8},−\mathrm{6} \\ $$$${since}\:{the}\:{line}\:{is}\:{slanted}\:{at}\:\mathrm{45}°,\:{then}: \\ $$$${x}=\mathrm{8}\sqrt{\mathrm{2}},\:{y}=\mathrm{6}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{x}+{y}=\mathrm{14}\sqrt{\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 29/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
