Menu Close

Question-174327

Tinku Tara 0 Comments
Pin




Question Number 174327 by aminee last updated on 30/Jul/22
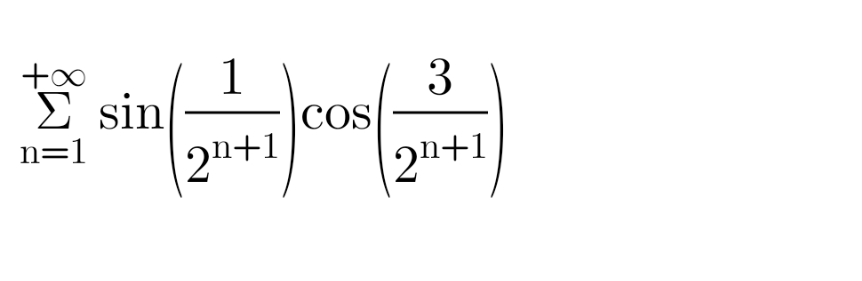
Answered by Mathspace last updated on 31/Jul/22
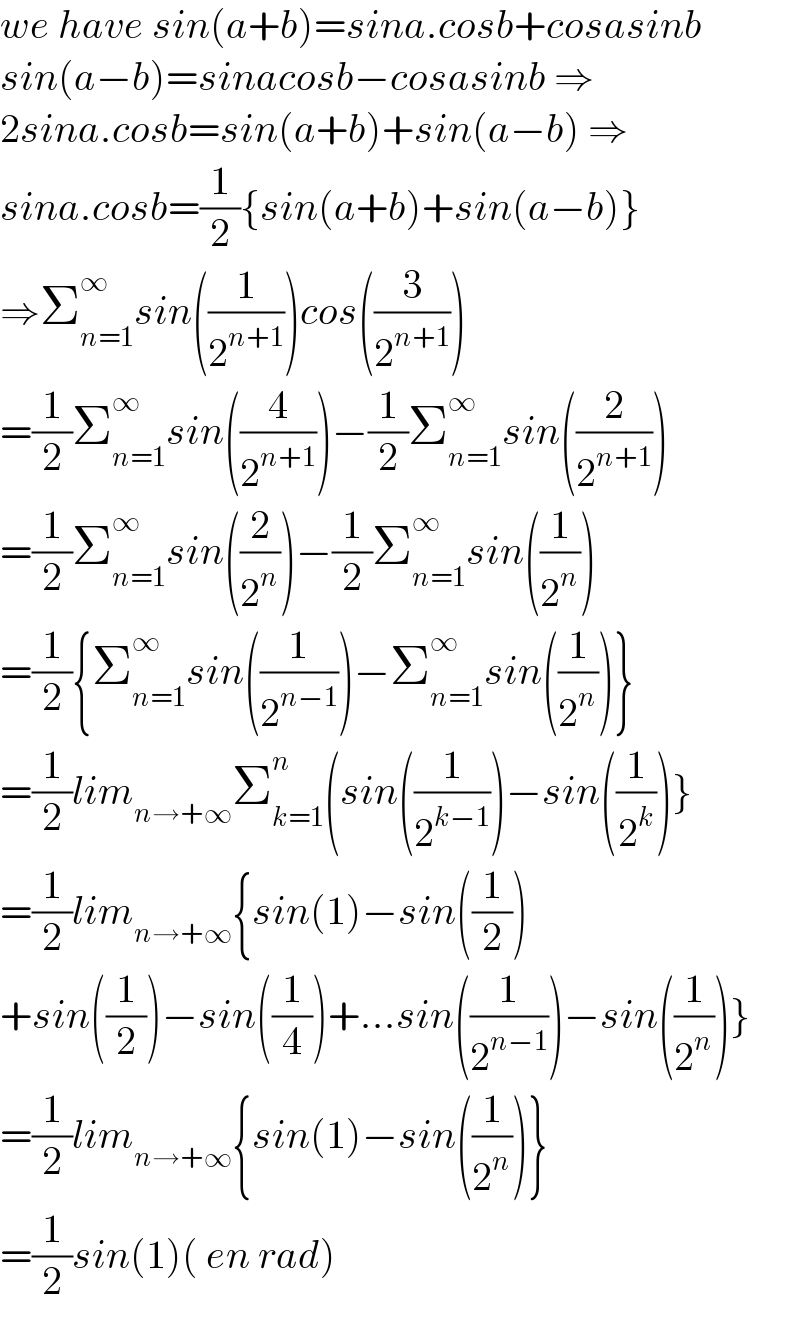
we have sin(a+b)=sina.cosb+cosasinb sin(a−b)=sinacosb−cosasinb ⇒ 2sina.cosb=sin(a+b)+sin(a−b) ⇒ sina.cosb=(1/2){sin(a+b)+sin(a−b)} ⇒Σ_(n=1) ^∞ sin((1/2^(n+1) ))cos((3/2^(n+1) )) =(1/2)Σ_(n=1) ^∞ sin((4/2^(n+1) ))−(1/2)Σ_(n=1) ^∞ sin((2/2^(n+1) )) =(1/2)Σ_(n=1) ^∞ sin((2/2^n ))−(1/2)Σ_(n=1) ^∞ sin((1/2^n )) =(1/2){Σ_(n=1) ^∞ sin((1/2^(n−1) ))−Σ_(n=1) ^∞ sin((1/2^n ))} =(1/2)lim_(n→+∞) Σ_(k=1) ^n (sin((1/2^(k−1) ))−sin((1/2^k ))} =(1/2)lim_(n→+∞) {sin(1)−sin((1/2)) +sin((1/2))−sin((1/4))+...sin((1/2^(n−1) ))−sin((1/2^n ))} =(1/2)lim_(n→+∞) {sin(1)−sin((1/2^n ))} =(1/2)sin(1)( en rad)
$${we}\:{have}\:{sin}\left({a}+{b}\right)={sina}.{cosb}+{cosasinb} \\ $$$${sin}\left({a}−{b}\right)={sinacosb}−{cosasinb}\:\Rightarrow \\ $$$$\mathrm{2}{sina}.{cosb}={sin}\left({a}+{b}\right)+{sin}\left({a}−{b}\right)\:\Rightarrow \\ $$$${sina}.{cosb}=\frac{\mathrm{1}}{\mathrm{2}}\left\{{sin}\left({a}+{b}\right)+{sin}\left({a}−{b}\right)\right\} \\ $$$$\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} {sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }\right){cos}\left(\frac{\mathrm{3}}{\mathrm{2}^{{n}+\mathrm{1}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} {sin}\left(\frac{\mathrm{4}}{\mathrm{2}^{{n}+\mathrm{1}} }\right)−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} {sin}\left(\frac{\mathrm{2}}{\mathrm{2}^{{n}+\mathrm{1}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} {sin}\left(\frac{\mathrm{2}}{\mathrm{2}^{{n}} }\right)−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} {sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\sum_{{n}=\mathrm{1}} ^{\infty} {sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\right)−\sum_{{n}=\mathrm{1}} ^{\infty} {sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{lim}_{{n}\rightarrow+\infty} \sum_{{k}=\mathrm{1}} ^{{n}} \left({sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{k}−\mathrm{1}} }\right)−{sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{lim}_{{n}\rightarrow+\infty} \left\{{sin}\left(\mathrm{1}\right)−{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right. \\ $$$$\left.+{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−{sin}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)+…{sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\right)−{sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{lim}_{{n}\rightarrow+\infty} \left\{{sin}\left(\mathrm{1}\right)−{sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{1}\right)\left(\:{en}\:{rad}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *