Question Number 174377 by AgniMath last updated on 31/Jul/22
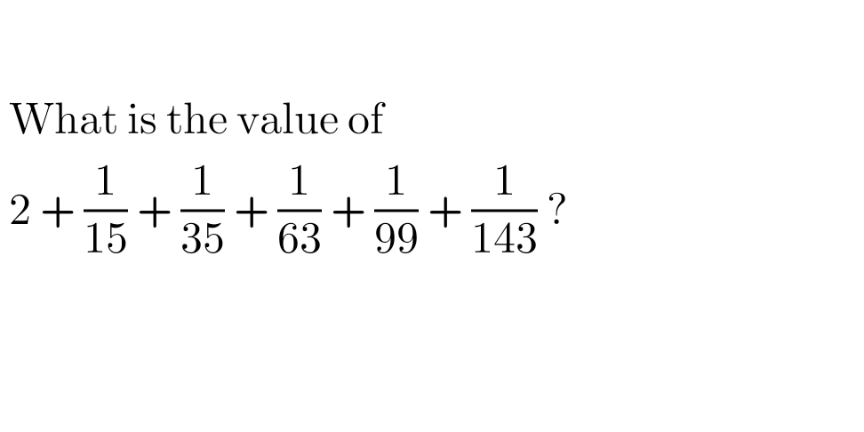
Answered by okbruh123 last updated on 31/Jul/22
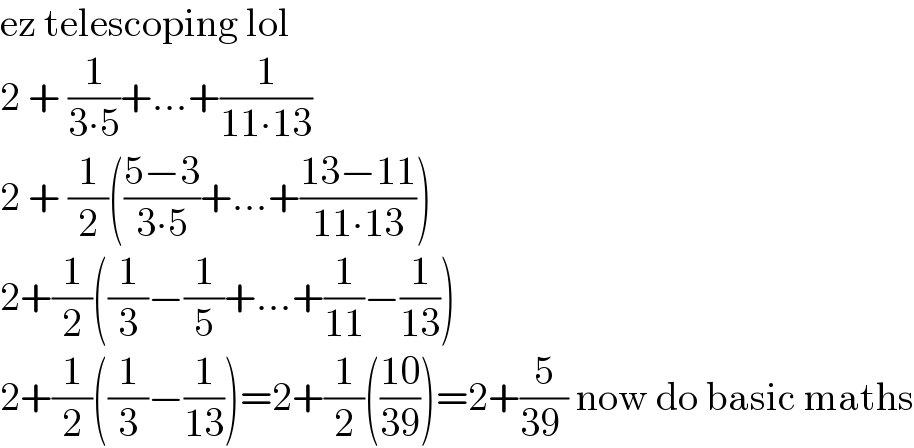
$$\mathrm{ez}\:\mathrm{telescoping}\:\mathrm{lol} \\ $$$$\mathrm{2}\:+\:\frac{\mathrm{1}}{\mathrm{3}\centerdot\mathrm{5}}+…+\frac{\mathrm{1}}{\mathrm{11}\centerdot\mathrm{13}} \\ $$$$\mathrm{2}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{5}−\mathrm{3}}{\mathrm{3}\centerdot\mathrm{5}}+…+\frac{\mathrm{13}−\mathrm{11}}{\mathrm{11}\centerdot\mathrm{13}}\right) \\ $$$$\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}+…+\frac{\mathrm{1}}{\mathrm{11}}−\frac{\mathrm{1}}{\mathrm{13}}\right) \\ $$$$\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{13}}\right)=\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{10}}{\mathrm{39}}\right)=\mathrm{2}+\frac{\mathrm{5}}{\mathrm{39}\:}\:\mathrm{now}\:\mathrm{do}\:\mathrm{basic}\:\mathrm{maths} \\ $$
