Question Number 174396 by Best1 last updated on 31/Jul/22
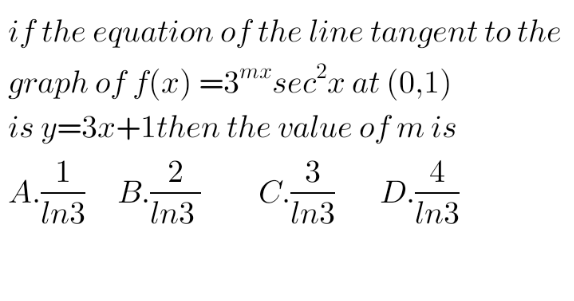
Answered by som(math1967) last updated on 31/Jul/22
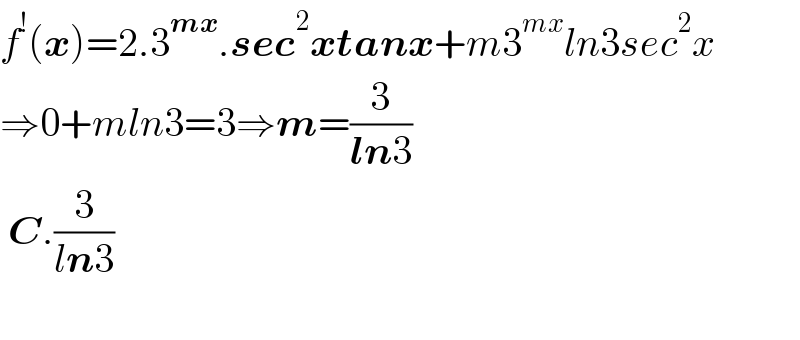
$${f}^{!} \left(\boldsymbol{{x}}\right)=\mathrm{2}.\mathrm{3}^{\boldsymbol{{mx}}} .\boldsymbol{{sec}}^{\mathrm{2}} \boldsymbol{{xtanx}}+{m}\mathrm{3}^{{mx}} {ln}\mathrm{3}{sec}^{\mathrm{2}} {x} \\ $$$$\Rightarrow\mathrm{0}+{mln}\mathrm{3}=\mathrm{3}\Rightarrow\boldsymbol{{m}}=\frac{\mathrm{3}}{\boldsymbol{{ln}}\mathrm{3}} \\ $$$$\:\boldsymbol{{C}}.\frac{\mathrm{3}}{{l}\boldsymbol{{n}}\mathrm{3}}\: \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 01/Aug/22
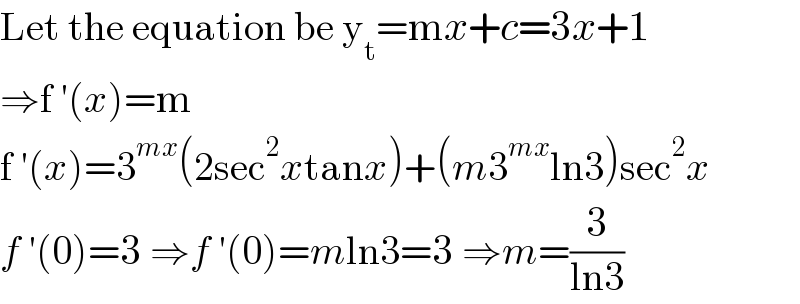
$$\mathrm{Let}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{be}\:\mathrm{y}_{\mathrm{t}} =\mathrm{m}{x}+{c}=\mathrm{3}{x}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{f}\:'\left({x}\right)=\mathrm{m} \\ $$$$\mathrm{f}\:'\left({x}\right)=\mathrm{3}^{{mx}} \left(\mathrm{2sec}^{\mathrm{2}} {x}\mathrm{tan}{x}\right)+\left({m}\mathrm{3}^{{mx}} \mathrm{ln3}\right)\mathrm{sec}^{\mathrm{2}} {x} \\ $$$${f}\:'\left(\mathrm{0}\right)=\mathrm{3}\:\Rightarrow{f}\:'\left(\mathrm{0}\right)={m}\mathrm{ln3}=\mathrm{3}\:\Rightarrow{m}=\frac{\mathrm{3}}{\mathrm{ln3}} \\ $$
Commented by Best1 last updated on 31/Jul/22
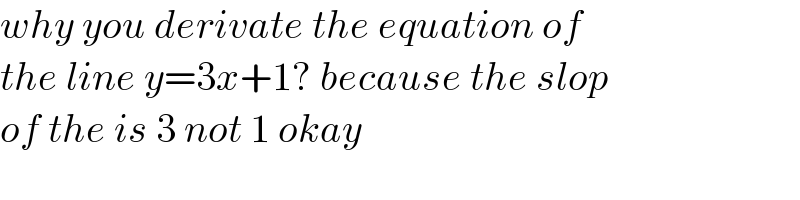
$${why}\:{you}\:{derivate}\:{the}\:{equation}\:{of}\: \\ $$$${the}\:{line}\:{y}=\mathrm{3}{x}+\mathrm{1}?\:{because}\:{the}\:{slop}\: \\ $$$${of}\:{the}\:{is}\:\mathrm{3}\:{not}\:\mathrm{1}\:{okay} \\ $$
Commented by som(math1967) last updated on 31/Jul/22
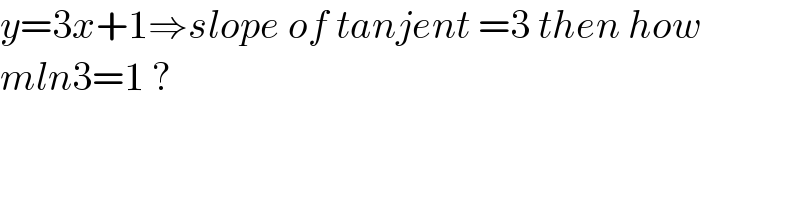
$${y}=\mathrm{3}{x}+\mathrm{1}\Rightarrow{slope}\:{of}\:{tanjent}\:=\mathrm{3}\:{then}\:{how} \\ $$$${mln}\mathrm{3}=\mathrm{1}\:? \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 01/Aug/22
$$\mathrm{You}'\mathrm{re}\:\mathrm{right}\:!\:\mathrm{Thanks}. \\ $$
