Question Number 174442 by oustmuchiya@gmail.com last updated on 01/Aug/22
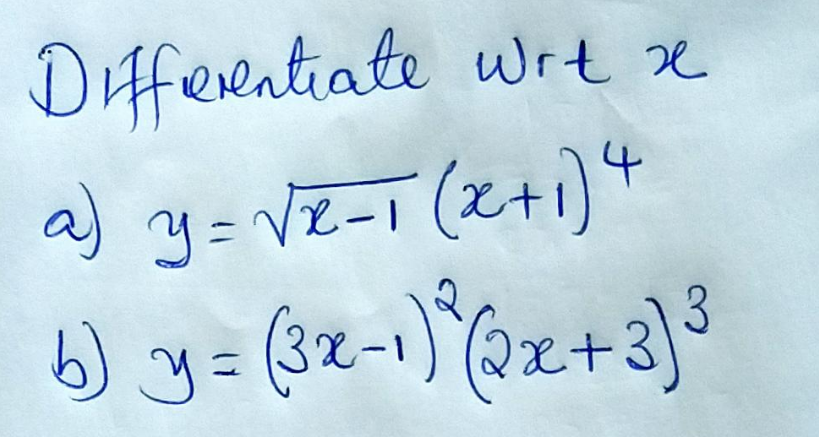
Answered by floor(10²Eta[1]) last updated on 01/Aug/22
![a) y′=(((x+1)^4 )/(2(√(x−1))))+4(x+1)^3 (√(x−1)) (x+1)^3 [((x+1)/(2(√(x−1))))+4(√(x−1))] (x+1)^3 (((9x−7)/(2(√(x−1))))) b) y′=6(3x−1)(2x+3)^3 +6(2x+3)^2 (3x−1)^2 =6(3x−1)(2x+3)^2 [(2x+3)+(3x−1)] =6(3x−1)(2x+3)^2 (5x+2)](https://www.tinkutara.com/question/Q174449.png)
$$\left.\mathrm{a}\right)\: \\ $$$$\mathrm{y}'=\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }{\mathrm{2}\sqrt{\mathrm{x}−\mathrm{1}}}+\mathrm{4}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \sqrt{\mathrm{x}−\mathrm{1}} \\ $$$$\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left[\frac{\mathrm{x}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}−\mathrm{1}}}+\mathrm{4}\sqrt{\mathrm{x}−\mathrm{1}}\right] \\ $$$$\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left(\frac{\mathrm{9x}−\mathrm{7}}{\mathrm{2}\sqrt{\mathrm{x}−\mathrm{1}}}\right) \\ $$$$\left.\mathrm{b}\right) \\ $$$$\mathrm{y}'=\mathrm{6}\left(\mathrm{3x}−\mathrm{1}\right)\left(\mathrm{2x}+\mathrm{3}\right)^{\mathrm{3}} +\mathrm{6}\left(\mathrm{2x}+\mathrm{3}\right)^{\mathrm{2}} \left(\mathrm{3x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\mathrm{6}\left(\mathrm{3x}−\mathrm{1}\right)\left(\mathrm{2x}+\mathrm{3}\right)^{\mathrm{2}} \left[\left(\mathrm{2x}+\mathrm{3}\right)+\left(\mathrm{3x}−\mathrm{1}\right)\right] \\ $$$$=\mathrm{6}\left(\mathrm{3x}−\mathrm{1}\right)\left(\mathrm{2x}+\mathrm{3}\right)^{\mathrm{2}} \left(\mathrm{5x}+\mathrm{2}\right) \\ $$
