Menu Close

Question-174552

Tinku Tara 0 Comments
Pin




Question Number 174552 by Tawa11 last updated on 03/Aug/22
Commented by Rasheed.Sindhi last updated on 04/Aug/22
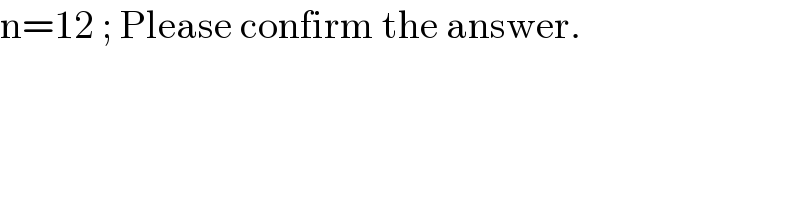
n=12 ; Please confirm the answer.
$$\mathrm{n}=\mathrm{12}\:;\:\mathrm{Please}\:\mathrm{confirm}\:\mathrm{the}\:\mathrm{answer}. \\ $$
Commented by Tawa11 last updated on 04/Aug/22
I don′t know the answer sir. please workings to follow.
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{sir}. \\ $$$$\mathrm{please}\:\mathrm{workings}\:\mathrm{to}\:\mathrm{follow}. \\ $$
Commented by Tawa11 last updated on 04/Aug/22
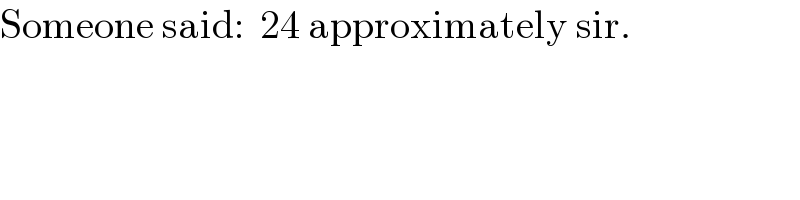
Someone said: 24 approximately sir.
$$\mathrm{Someone}\:\mathrm{said}:\:\:\mathrm{24}\:\mathrm{approximately}\:\mathrm{sir}. \\ $$
Answered by Rasheed.Sindhi last updated on 05/Aug/22
AnOther way t is only for comparison its value doesn′t matter. Let for convenience t=gcd(46,69)=23 Number of vegitables per minute determinant (((rad. ),(cucum.),(onions),(okra )),((((46)/(23))=2),(((46)/(23))=2),(((69)/(23))=3),(((69)/(23))=3))) Number of minutes per vegitable determinant (((rad. ),(cucum.),(onions),(okra )),((((23)/(46))=(1/2)),(((23)/(46))=(1/2)),(((23)/(69))=(1/3)),(((23)/(69))=(1/3)))) First k minutes k/4 minutes for each vegitable determinant ((,(rad. ),(cucu.),(onions),(okra )),((per min.),2,2,3,3),((in (k/4) mins),(((2k)/4)=(k/2)),(((2k)/4)=(k/2)),((3k)/4),((3k)/4))) 2((k/2))+2(((3k)/4))=((5k)/2) vegitables. Next k minutes n+n+n+n=4n vegitables time in each vegitable: determinant ((,(rad. ),(cucum.),(onions),(okra )),((per veg._(time) ),(1/2),(1/2),(1/3),(1/3)),((time in_(n vegs) ),(n/2),(n/2),(n/3),(n/3))) total time: 2((n/2))+2((n/3))=((5n)/3)=k In 2k minutes total vegitables: ((5k)/2)+4n=98 (5/2)∙((5n)/3)+4n=98 [∵ k=((5n)/3)] ((49n)/6)=98 n=((98×6)/(49))=12
$$\mathrm{AnOther}\:\mathrm{way} \\ $$$$\boldsymbol{\mathrm{t}}\:\mathrm{is}\:\mathrm{only}\:\mathrm{for}\:\mathrm{comparison}\:\mathrm{its}\:\mathrm{value}\: \\ $$$$\mathrm{doesn}'\mathrm{t}\:\mathrm{matter}. \\ $$$$\mathrm{Let}\:\mathrm{for}\:\mathrm{convenience}\:\mathrm{t}=\mathrm{gcd}\left(\mathrm{46},\mathrm{69}\right)=\mathrm{23} \\ $$$$\underline{\mathrm{Number}\:\mathrm{of}\:\mathrm{vegitables}\:\mathrm{per}\:\mathrm{minute}} \\ $$$$\begin{array}{|c|c|}{\mathrm{rad}.\:\:\:\:}&\hline{\mathrm{cucum}.}&\hline{\mathrm{onions}}&\hline{\mathrm{okra}\:\:}\\{\frac{\mathrm{46}}{\mathrm{23}}=\mathrm{2}}&\hline{\frac{\mathrm{46}}{\mathrm{23}}=\mathrm{2}}&\hline{\frac{\mathrm{69}}{\mathrm{23}}=\mathrm{3}}&\hline{\frac{\mathrm{69}}{\mathrm{23}}=\mathrm{3}}\\\hline\end{array}\: \\ $$$$ \\ $$$$\underline{\mathrm{Number}\:\mathrm{of}\:\mathrm{minutes}\:\mathrm{per}\:\mathrm{vegitable}} \\ $$$$\begin{array}{|c|c|}{\mathrm{rad}.\:\:\:\:}&\hline{\mathrm{cucum}.}&\hline{\mathrm{onions}}&\hline{\mathrm{okra}\:\:}\\{\frac{\mathrm{23}}{\mathrm{46}}=\frac{\mathrm{1}}{\mathrm{2}}}&\hline{\frac{\mathrm{23}}{\mathrm{46}}=\frac{\mathrm{1}}{\mathrm{2}}}&\hline{\frac{\mathrm{23}}{\mathrm{69}}=\frac{\mathrm{1}}{\mathrm{3}}}&\hline{\frac{\mathrm{23}}{\mathrm{69}}=\frac{\mathrm{1}}{\mathrm{3}}}\\\hline\end{array}\: \\ $$$$ \\ $$$$\underline{\mathrm{First}\:\mathrm{k}\:\mathrm{minutes}} \\ $$$$\mathrm{k}/\mathrm{4}\:\mathrm{minutes}\:\mathrm{for}\:\mathrm{each}\:\mathrm{vegitable} \\ $$$$\begin{array}{|c|c|c|}{}&\hline{\mathrm{rad}.\:\:\:\:}&\hline{\mathrm{cucu}.}&\hline{\mathrm{onions}}&\hline{\mathrm{okra}\:\:}\\{\mathrm{per}\:\mathrm{min}.}&\hline{\mathrm{2}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}&\hline{\mathrm{3}}\\{\mathrm{in}\:\frac{\mathrm{k}}{\mathrm{4}}\:\mathrm{mins}}&\hline{\frac{\mathrm{2k}}{\mathrm{4}}=\frac{\mathrm{k}}{\mathrm{2}}}&\hline{\frac{\mathrm{2k}}{\mathrm{4}}=\frac{\mathrm{k}}{\mathrm{2}}}&\hline{\frac{\mathrm{3k}}{\mathrm{4}}}&\hline{\frac{\mathrm{3k}}{\mathrm{4}}}\\\hline\end{array}\: \\ $$$$\mathrm{2}\left(\frac{\mathrm{k}}{\mathrm{2}}\right)+\mathrm{2}\left(\frac{\mathrm{3k}}{\mathrm{4}}\right)=\frac{\mathrm{5k}}{\mathrm{2}}\:\:\mathrm{vegitables}. \\ $$$$\underline{\mathrm{Next}\:\mathrm{k}\:\mathrm{minutes}} \\ $$$$\:\mathrm{n}+\mathrm{n}+\mathrm{n}+\mathrm{n}=\mathrm{4n}\:\mathrm{vegitables} \\ $$$$\:\mathrm{time}\:\mathrm{in}\:\mathrm{each}\:\mathrm{vegitable}: \\ $$$$\begin{array}{|c|c|c|}{}&\hline{\mathrm{rad}.\:\:\:\:}&\hline{\mathrm{cucum}.}&\hline{\mathrm{onions}}&\hline{\mathrm{okra}\:\:}\\{\underset{\mathrm{time}} {\mathrm{per}\:\mathrm{veg}.}}&\hline{\mathrm{1}/\mathrm{2}}&\hline{\mathrm{1}/\mathrm{2}}&\hline{\mathrm{1}/\mathrm{3}}&\hline{\mathrm{1}/\mathrm{3}}\\{\underset{\mathrm{n}\:\mathrm{vegs}} {\mathrm{time}\:\mathrm{in}}}&\hline{\frac{\mathrm{n}}{\mathrm{2}}}&\hline{\frac{\mathrm{n}}{\mathrm{2}}}&\hline{\frac{\mathrm{n}}{\mathrm{3}}}&\hline{\frac{\mathrm{n}}{\mathrm{3}}}\\\hline\end{array} \\ $$$$\mathrm{total}\:\mathrm{time}:\:\:\:\:\:\mathrm{2}\left(\frac{\mathrm{n}}{\mathrm{2}}\right)+\mathrm{2}\left(\frac{\mathrm{n}}{\mathrm{3}}\right)=\frac{\mathrm{5n}}{\mathrm{3}}=\mathrm{k}\: \\ $$$$ \\ $$$$\underline{\mathrm{In}\:\mathrm{2k}\:\mathrm{minutes}} \\ $$$$\mathrm{total}\:\mathrm{vegitables}: \\ $$$$\frac{\mathrm{5k}}{\mathrm{2}}+\mathrm{4n}=\mathrm{98} \\ $$$$\frac{\mathrm{5}}{\mathrm{2}}\centerdot\frac{\mathrm{5n}}{\mathrm{3}}+\mathrm{4n}=\mathrm{98}\:\:\:\left[\because\:\mathrm{k}=\frac{\mathrm{5n}}{\mathrm{3}}\right] \\ $$$$\frac{\mathrm{49n}}{\mathrm{6}}=\mathrm{98} \\ $$$$\:\:\:\:\:\mathrm{n}=\frac{\mathrm{98}×\mathrm{6}}{\mathrm{49}}=\mathrm{12} \\ $$
Commented by Tawa11 last updated on 05/Aug/22
God bless you sir. I appreciate.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Answered by Rasheed.Sindhi last updated on 05/Aug/22
Number of vegitables per minute determinant (((rad. ),(cucum.),(onions),(okra )),((46/t),(46/t),(69/t),(69/t))) Number of minutes per vegitable determinant (((rad. ),(cucum.),(onions),(okra )),((t/46),(t/46),(t/69),(t/69))) First k minutes k/4 minutes for each vegitable determinant ((,(rad. ),(cucu.),(onions),(okra )),((per min.),(46/t),(46/t),(69/t),(69/t)),((in (k/4) mins),((46k)/(4t)),((46k)/(4t)),((69k)/(4t)),((69k)/(4t)))) 2(((46k)/(4t)))+2(((69k)/(4t))) vegitables. Next k minutes n+n+n+n=4n vegitables time in each vegitable: determinant ((,(rad. ),(cucum.),(onions),(okra )),((per veg._(time) ),(t/46),(t/46),(t/69),(t/69)),((time in_(n vegs) ),((nt)/(46)),((nt)/(46)),((nt)/(69)),((nt)/(69)))) total time: 2(((nt)/(46)))+2(((nt)/(69)))=k In 2k minutes total vegitables: 2(((46k)/(4t)))+2(((69k)/(4t)))+4n=98 k(((46)/(2t))+((69)/(2t)))+4n=98 ∵ k=2(((nt)/(46)))+2(((nt)/(69))) from above. ∴ (2(((nt)/(46)))+2(((nt)/(69))))(((46)/(2t))+((69)/(2t)))+4n=98 t(2((n/(46)))+2((n/(69))))∙(1/t)(((46)/2)+((69)/2))+4n=98 ((n/(23))+((2n)/(69)))(((115)/2))+4n=98 (((25)/6)+4)n=98 ((49)/6)n=98 n=((98×6)/(49))=12
$$\underline{\mathrm{Number}\:\mathrm{of}\:\mathrm{vegitables}\:\mathrm{per}\:\mathrm{minute}} \\ $$$$\begin{array}{|c|c|}{\mathrm{rad}.\:\:\:\:}&\hline{\mathrm{cucum}.}&\hline{\mathrm{onions}}&\hline{\mathrm{okra}\:\:}\\{\mathrm{46}/\mathrm{t}}&\hline{\mathrm{46}/\mathrm{t}}&\hline{\mathrm{69}/\mathrm{t}}&\hline{\mathrm{69}/\mathrm{t}}\\\hline\end{array}\: \\ $$$$ \\ $$$$\underline{\mathrm{Number}\:\mathrm{of}\:\mathrm{minutes}\:\mathrm{per}\:\mathrm{vegitable}} \\ $$$$\begin{array}{|c|c|}{\mathrm{rad}.\:\:\:\:}&\hline{\mathrm{cucum}.}&\hline{\mathrm{onions}}&\hline{\mathrm{okra}\:\:}\\{\mathrm{t}/\mathrm{46}}&\hline{\mathrm{t}/\mathrm{46}}&\hline{\mathrm{t}/\mathrm{69}}&\hline{\mathrm{t}/\mathrm{69}}\\\hline\end{array}\: \\ $$$$ \\ $$$$\underline{\mathrm{First}\:\mathrm{k}\:\mathrm{minutes}} \\ $$$$\mathrm{k}/\mathrm{4}\:\mathrm{minutes}\:\mathrm{for}\:\mathrm{each}\:\mathrm{vegitable} \\ $$$$\begin{array}{|c|c|c|}{}&\hline{\mathrm{rad}.\:\:\:\:}&\hline{\mathrm{cucu}.}&\hline{\mathrm{onions}}&\hline{\mathrm{okra}\:\:}\\{\mathrm{per}\:\mathrm{min}.}&\hline{\mathrm{46}/\mathrm{t}}&\hline{\mathrm{46}/\mathrm{t}}&\hline{\mathrm{69}/\mathrm{t}}&\hline{\mathrm{69}/\mathrm{t}}\\{\mathrm{in}\:\frac{\mathrm{k}}{\mathrm{4}}\:\mathrm{mins}}&\hline{\frac{\mathrm{46k}}{\mathrm{4t}}}&\hline{\frac{\mathrm{46k}}{\mathrm{4t}}}&\hline{\frac{\mathrm{69k}}{\mathrm{4t}}}&\hline{\frac{\mathrm{69k}}{\mathrm{4t}}}\\\hline\end{array}\: \\ $$$$\mathrm{2}\left(\frac{\mathrm{46k}}{\mathrm{4t}}\right)+\mathrm{2}\left(\frac{\mathrm{69k}}{\mathrm{4t}}\right)\:\mathrm{vegitables}. \\ $$$$\underline{\mathrm{Next}\:\mathrm{k}\:\mathrm{minutes}} \\ $$$$\:\mathrm{n}+\mathrm{n}+\mathrm{n}+\mathrm{n}=\mathrm{4n}\:\mathrm{vegitables} \\ $$$$\:\mathrm{time}\:\mathrm{in}\:\mathrm{each}\:\mathrm{vegitable}: \\ $$$$\begin{array}{|c|c|c|}{}&\hline{\mathrm{rad}.\:\:\:\:}&\hline{\mathrm{cucum}.}&\hline{\mathrm{onions}}&\hline{\mathrm{okra}\:\:}\\{\underset{\mathrm{time}} {\mathrm{per}\:\mathrm{veg}.}}&\hline{\mathrm{t}/\mathrm{46}}&\hline{\mathrm{t}/\mathrm{46}}&\hline{\mathrm{t}/\mathrm{69}}&\hline{\mathrm{t}/\mathrm{69}}\\{\underset{\mathrm{n}\:\mathrm{vegs}} {\mathrm{time}\:\mathrm{in}}}&\hline{\frac{\mathrm{nt}}{\mathrm{46}}}&\hline{\frac{\mathrm{nt}}{\mathrm{46}}}&\hline{\frac{\mathrm{nt}}{\mathrm{69}}}&\hline{\frac{\mathrm{nt}}{\mathrm{69}}}\\\hline\end{array} \\ $$$$\mathrm{total}\:\mathrm{time}:\:\:\:\:\:\mathrm{2}\left(\frac{\mathrm{nt}}{\mathrm{46}}\right)+\mathrm{2}\left(\frac{\mathrm{nt}}{\mathrm{69}}\right)=\mathrm{k}\: \\ $$$$ \\ $$$$\underline{\mathrm{In}\:\mathrm{2k}\:\mathrm{minutes}} \\ $$$$\mathrm{total}\:\mathrm{vegitables}: \\ $$$$\mathrm{2}\left(\frac{\mathrm{46k}}{\mathrm{4t}}\right)+\mathrm{2}\left(\frac{\mathrm{69k}}{\mathrm{4t}}\right)+\mathrm{4n}=\mathrm{98} \\ $$$$\mathrm{k}\left(\frac{\mathrm{46}}{\mathrm{2t}}+\frac{\mathrm{69}}{\mathrm{2t}}\right)+\mathrm{4n}=\mathrm{98}\: \\ $$$$\because\:\:\mathrm{k}=\mathrm{2}\left(\frac{\mathrm{nt}}{\mathrm{46}}\right)+\mathrm{2}\left(\frac{\mathrm{nt}}{\mathrm{69}}\right)\:\mathrm{from}\:\mathrm{above}. \\ $$$$\therefore\:\:\left(\mathrm{2}\left(\frac{\mathrm{nt}}{\mathrm{46}}\right)+\mathrm{2}\left(\frac{\mathrm{nt}}{\mathrm{69}}\right)\right)\left(\frac{\mathrm{46}}{\mathrm{2t}}+\frac{\mathrm{69}}{\mathrm{2t}}\right)+\mathrm{4n}=\mathrm{98} \\ $$$$\cancel{\mathrm{t}}\left(\mathrm{2}\left(\frac{\mathrm{n}}{\mathrm{46}}\right)+\mathrm{2}\left(\frac{\mathrm{n}}{\mathrm{69}}\right)\right)\centerdot\frac{\mathrm{1}}{\cancel{\mathrm{t}}}\left(\frac{\mathrm{46}}{\mathrm{2}}+\frac{\mathrm{69}}{\mathrm{2}}\right)+\mathrm{4n}=\mathrm{98} \\ $$$$\left(\frac{\mathrm{n}}{\mathrm{23}}+\frac{\mathrm{2n}}{\mathrm{69}}\right)\left(\frac{\mathrm{115}}{\mathrm{2}}\right)+\mathrm{4n}=\mathrm{98} \\ $$$$\left(\frac{\mathrm{25}}{\mathrm{6}}+\mathrm{4}\right)\mathrm{n}=\mathrm{98} \\ $$$$\frac{\mathrm{49}}{\mathrm{6}}\mathrm{n}=\mathrm{98} \\ $$$$\mathrm{n}=\frac{\mathrm{98}×\mathrm{6}}{\mathrm{49}}=\mathrm{12} \\ $$
Commented by Tawa11 last updated on 05/Aug/22
Wow, God bless you sir
$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *