Question Number 174619 by cortano1 last updated on 06/Aug/22

Answered by aleks041103 last updated on 06/Aug/22
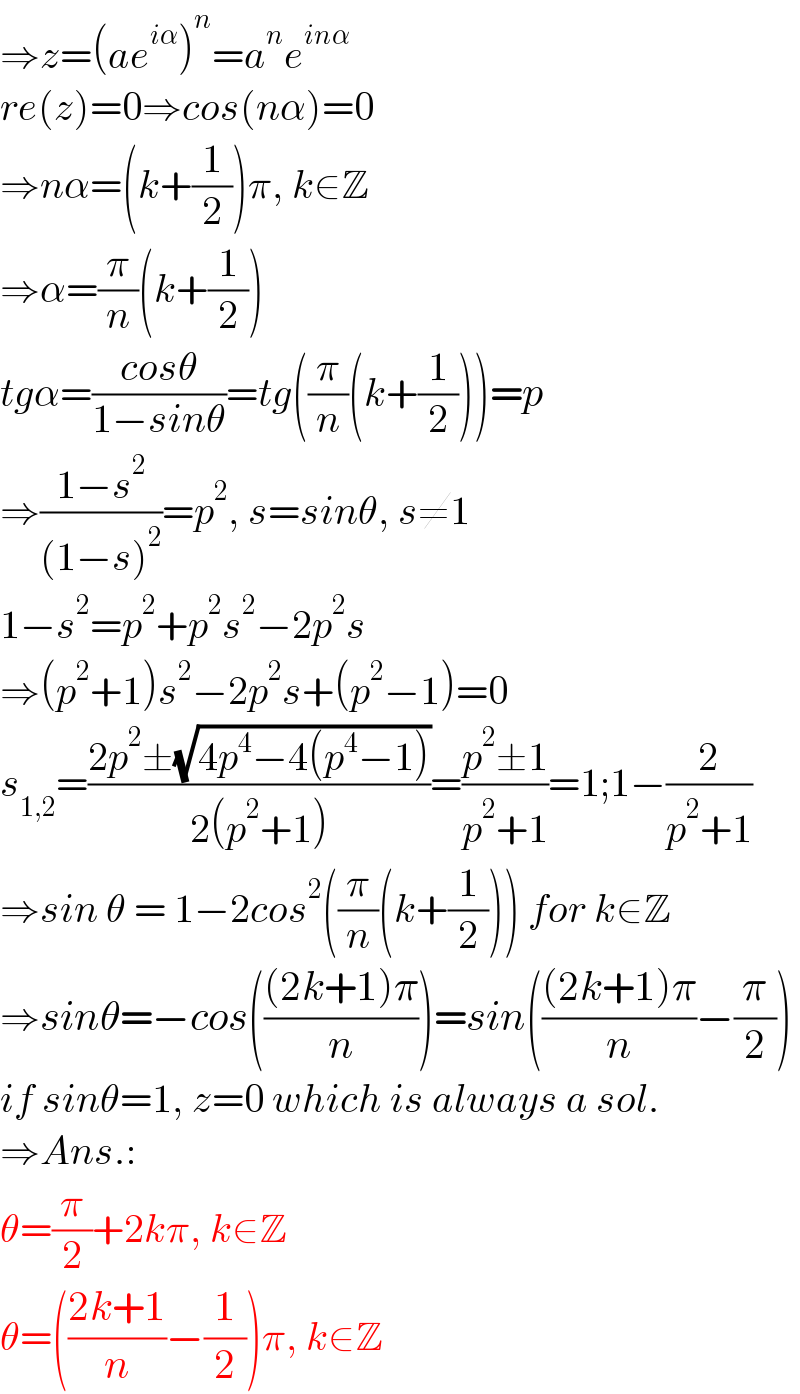
$$\Rightarrow{z}=\left({ae}^{{i}\alpha} \right)^{{n}} ={a}^{{n}} {e}^{{in}\alpha} \\ $$$${re}\left({z}\right)=\mathrm{0}\Rightarrow{cos}\left({n}\alpha\right)=\mathrm{0} \\ $$$$\Rightarrow{n}\alpha=\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)\pi,\:{k}\in\mathbb{Z} \\ $$$$\Rightarrow\alpha=\frac{\pi}{{n}}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${tg}\alpha=\frac{{cos}\theta}{\mathrm{1}−{sin}\theta}={tg}\left(\frac{\pi}{{n}}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)={p} \\ $$$$\Rightarrow\frac{\mathrm{1}−{s}^{\mathrm{2}} }{\left(\mathrm{1}−{s}\right)^{\mathrm{2}} }={p}^{\mathrm{2}} ,\:{s}={sin}\theta,\:{s}\neq\mathrm{1} \\ $$$$\mathrm{1}−{s}^{\mathrm{2}} ={p}^{\mathrm{2}} +{p}^{\mathrm{2}} {s}^{\mathrm{2}} −\mathrm{2}{p}^{\mathrm{2}} {s} \\ $$$$\Rightarrow\left({p}^{\mathrm{2}} +\mathrm{1}\right){s}^{\mathrm{2}} −\mathrm{2}{p}^{\mathrm{2}} {s}+\left({p}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$${s}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{2}{p}^{\mathrm{2}} \pm\sqrt{\mathrm{4}{p}^{\mathrm{4}} −\mathrm{4}\left({p}^{\mathrm{4}} −\mathrm{1}\right)}}{\mathrm{2}\left({p}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{{p}^{\mathrm{2}} \pm\mathrm{1}}{{p}^{\mathrm{2}} +\mathrm{1}}=\mathrm{1};\mathrm{1}−\frac{\mathrm{2}}{{p}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow{sin}\:\theta\:=\:\mathrm{1}−\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\pi}{{n}}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\:{for}\:{k}\in\mathbb{Z} \\ $$$$\Rightarrow{sin}\theta=−{cos}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}\right)={sin}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}−\frac{\pi}{\mathrm{2}}\right) \\ $$$${if}\:{sin}\theta=\mathrm{1},\:{z}=\mathrm{0}\:{which}\:{is}\:{always}\:{a}\:{sol}. \\ $$$$\Rightarrow{Ans}.: \\ $$$$\theta=\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi,\:{k}\in\mathbb{Z} \\ $$$$\theta=\left(\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\pi,\:{k}\in\mathbb{Z} \\ $$
Commented by Tawa11 last updated on 06/Aug/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by Mathspace last updated on 06/Aug/22

$${z}=\left(\mathrm{1}−{cos}\left(\frac{\pi}{\mathrm{2}}−\theta\right)+{isin}\left(\frac{\pi}{\mathrm{2}}−\theta\right)\right)^{{n}} \\ $$$$=\left(\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)+\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right){cos}\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)\right)^{{n}} \\ $$$$=\left(\mathrm{2}{i}\right)^{{n}} {sin}^{{n}} \left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)\left\{{cos}\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)−{isin}\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)\right\}^{{n}} \\ $$$$=\left(\mathrm{2}{i}\right)^{{n}} {sin}^{{n}} \left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right){e}^{{i}\left(\frac{{n}\pi}{\mathrm{4}}−\frac{{n}\theta}{\mathrm{2}}\right)} \\ $$$$=\mathrm{2}^{{n}} {sin}^{{n}} \left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right){e}^{{i}\frac{{n}\pi}{\mathrm{2}}+{i}\left(\frac{{n}\pi}{\mathrm{4}}−\frac{{n}\theta}{\mathrm{2}}\right)} \\ $$$$=\mathrm{2}^{{n}} {sin}^{{n}} \left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right){e}^{{i}\left(\frac{\mathrm{3}{n}\pi}{\mathrm{4}}−\frac{{n}\theta}{\mathrm{2}}\right)} \\ $$$${Res}\left({z}\right)=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{2}^{{n}} {sin}^{{n}} \left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right){cos}\left(\frac{\mathrm{3}{n}\pi}{\mathrm{4}}−\frac{{n}\theta}{\mathrm{2}}\right)=\mathrm{0}\:\Rightarrow \\ $$$${sin}\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)=\mathrm{0}\:{aur}\:{cos}\left(\frac{\mathrm{3}{n}\pi}{\mathrm{4}}−\frac{{n}\theta}{\mathrm{2}}\right)=\mathrm{0}\:\Rightarrow \\ $$$$\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}={k}\pi\:\:{aur}\:\frac{\mathrm{3}{n}\pi}{\mathrm{4}}−\frac{{n}\theta}{\mathrm{2}}=\frac{\pi}{\mathrm{2}}+{k}\pi\:\Rightarrow \\ $$$$\frac{\pi}{\mathrm{2}}−\theta=\mathrm{2}{k}\pi\:{aur}\:\frac{\mathrm{3}{n}\pi}{\mathrm{2}}−{n}\theta\:=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi \\ $$$$\Rightarrow\theta=\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi\:{aur}\:{n}\theta=\frac{\mathrm{3}{n}\pi}{\mathrm{2}}−\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\:\Rightarrow \\ $$$$\theta=\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi\:{aur}\:\theta=\frac{\mathrm{3}\pi}{\mathrm{2}}−\frac{\left.\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}} \\ $$
Commented by peter frank last updated on 06/Aug/22

$$\mathrm{thnk}\:\mathrm{you} \\ $$
