Question-174635

Question Number 174635 by mnjuly1970 last updated on 06/Aug/22

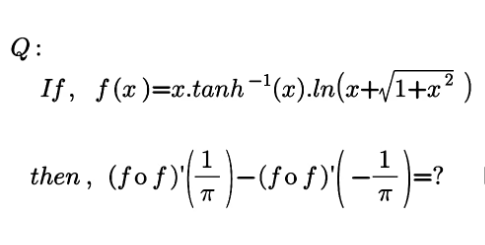
Answered by aleks041103 last updated on 06/Aug/22

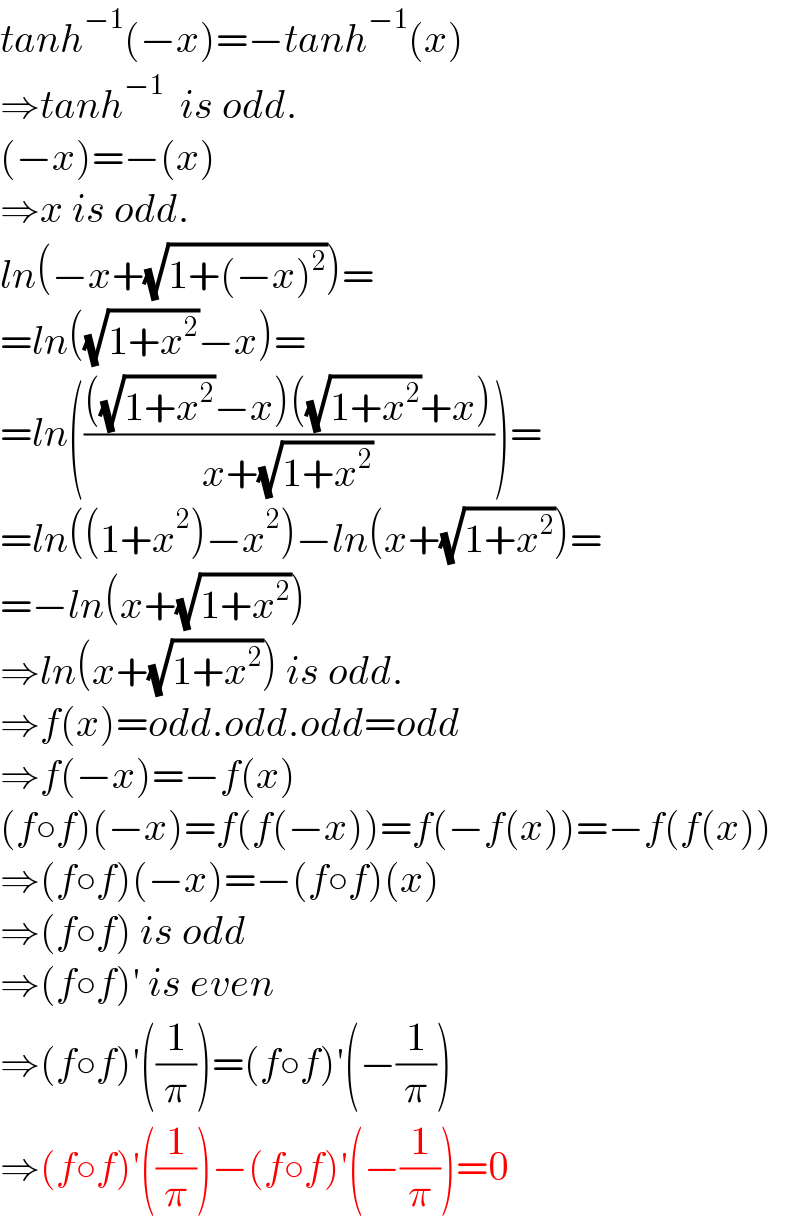
tanh^(−1) (−x)=−tanh^(−1) (x) ⇒tanh^(−1) is odd. (−x)=−(x) ⇒x is odd. ln(−x+(√(1+(−x)^2 )))= =ln((√(1+x^2 ))−x)= =ln(((((√(1+x^2 ))−x)((√(1+x^2 ))+x))/(x+(√(1+x^2 )))))= =ln((1+x^2 )−x^2 )−ln(x+(√(1+x^2 )))= =−ln(x+(√(1+x^2 ))) ⇒ln(x+(√(1+x^2 ))) is odd. ⇒f(x)=odd.odd.odd=odd ⇒f(−x)=−f(x) (f○f)(−x)=f(f(−x))=f(−f(x))=−f(f(x)) ⇒(f○f)(−x)=−(f○f)(x) ⇒(f○f) is odd ⇒(f○f)′ is even ⇒(f○f)′((1/π))=(f○f)′(−(1/π)) ⇒(f○f)′((1/π))−(f○f)′(−(1/π))=0

$${tanh}^{−\mathrm{1}} \left(−{x}\right)=−{tanh}^{−\mathrm{1}} \left({x}\right) \\ $$$$\Rightarrow{tanh}^{−\mathrm{1}} \:\:{is}\:{odd}. \\ $$$$\left(−{x}\right)=−\left({x}\right) \\ $$$$\Rightarrow{x}\:{is}\:{odd}. \\ $$$${ln}\left(−{x}+\sqrt{\mathrm{1}+\left(−{x}\right)^{\mathrm{2}} }\right)= \\ $$$$={ln}\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−{x}\right)= \\ $$$$={ln}\left(\frac{\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−{x}\right)\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+{x}\right)}{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)= \\ $$$$={ln}\left(\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−{x}^{\mathrm{2}} \right)−{ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)= \\ $$$$=−{ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:{is}\:{odd}. \\ $$$$\Rightarrow{f}\left({x}\right)={odd}.{odd}.{odd}={odd} \\ $$$$\Rightarrow{f}\left(−{x}\right)=−{f}\left({x}\right) \\ $$$$\left({f}\circ{f}\right)\left(−{x}\right)={f}\left({f}\left(−{x}\right)\right)={f}\left(−{f}\left({x}\right)\right)=−{f}\left({f}\left({x}\right)\right) \\ $$$$\Rightarrow\left({f}\circ{f}\right)\left(−{x}\right)=−\left({f}\circ{f}\right)\left({x}\right) \\ $$$$\Rightarrow\left({f}\circ{f}\right)\:{is}\:{odd} \\ $$$$\Rightarrow\left({f}\circ{f}\right)'\:{is}\:{even} \\ $$$$\Rightarrow\left({f}\circ{f}\right)'\left(\frac{\mathrm{1}}{\pi}\right)=\left({f}\circ{f}\right)'\left(−\frac{\mathrm{1}}{\pi}\right) \\ $$$$\Rightarrow\left({f}\circ{f}\right)'\left(\frac{\mathrm{1}}{\pi}\right)−\left({f}\circ{f}\right)'\left(−\frac{\mathrm{1}}{\pi}\right)=\mathrm{0} \\ $$

Commented by mnjuly1970 last updated on 06/Aug/22

$$\:\:{great}\:…{excellent} \\ $$

Answered by Mathspace last updated on 06/Aug/22

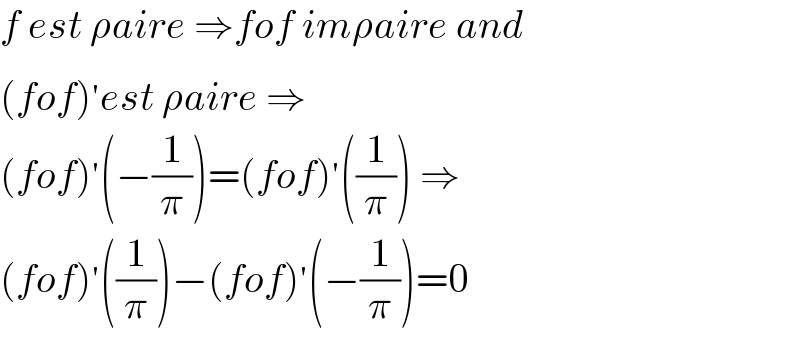
f est ρaire ⇒fof imρaire and (fof)^′ est ρaire ⇒ (fof)^′ (−(1/π))=(fof)^′ ((1/π)) ⇒ (fof)^′ ((1/π))−(fof)^′ (−(1/π))=0

$${f}\:{est}\:\rho{aire}\:\Rightarrow{fof}\:{im}\rho{aire}\:{and} \\ $$$$\left({fof}\right)^{'} {est}\:\rho{aire}\:\Rightarrow \\ $$$$\left({fof}\right)^{'} \left(−\frac{\mathrm{1}}{\pi}\right)=\left({fof}\right)^{'} \left(\frac{\mathrm{1}}{\pi}\right)\:\Rightarrow \\ $$$$\left({fof}\right)^{'} \left(\frac{\mathrm{1}}{\pi}\right)−\left({fof}\right)^{'} \left(−\frac{\mathrm{1}}{\pi}\right)=\mathrm{0} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply