Question-174666

Question Number 174666 by mnjuly1970 last updated on 07/Aug/22

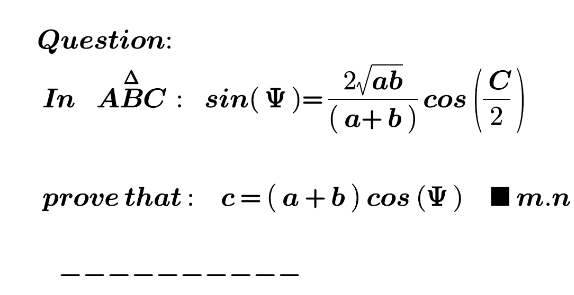
Answered by behi834171 last updated on 08/Aug/22

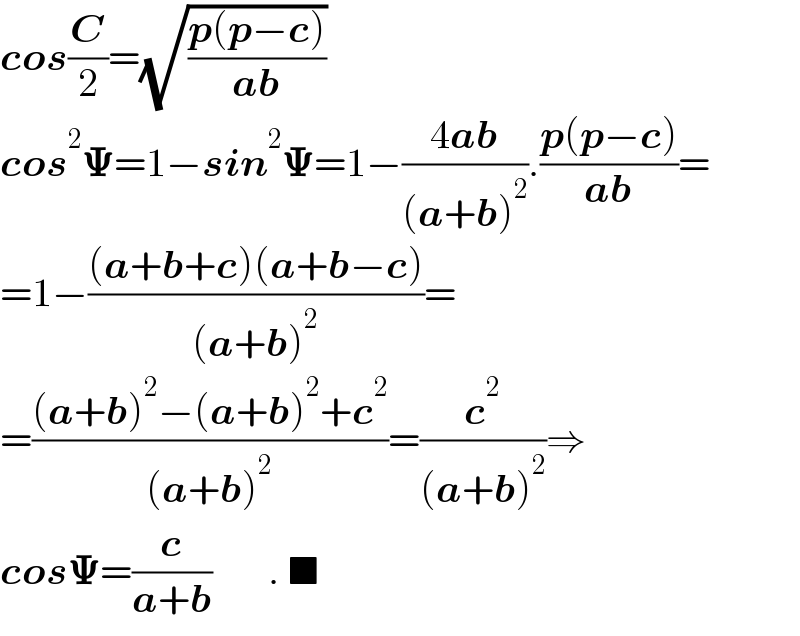
cos(C/2)=(√((p(p−c))/(ab))) cos^2 𝚿=1−sin^2 𝚿=1−((4ab)/((a+b)^2 )).((p(p−c))/(ab))= =1−(((a+b+c)(a+b−c))/((a+b)^2 ))= =(((a+b)^2 −(a+b)^2 +c^2 )/((a+b)^2 ))=(c^2 /((a+b)^2 ))⇒ cos𝚿=(c/(a+b)) . ■

$$\boldsymbol{{cos}}\frac{\boldsymbol{{C}}}{\mathrm{2}}=\sqrt{\frac{\boldsymbol{{p}}\left(\boldsymbol{{p}}−\boldsymbol{{c}}\right)}{\boldsymbol{{ab}}}} \\ $$$$\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{\Psi}=\mathrm{1}−\boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{\Psi}=\mathrm{1}−\frac{\mathrm{4}\boldsymbol{{ab}}}{\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} }.\frac{\boldsymbol{{p}}\left(\boldsymbol{{p}}−\boldsymbol{{c}}\right)}{\boldsymbol{{ab}}}= \\ $$$$=\mathrm{1}−\frac{\left(\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{b}}−\boldsymbol{{c}}\right)}{\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} }= \\ $$$$=\frac{\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} −\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} }{\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} }=\frac{\boldsymbol{{c}}^{\mathrm{2}} }{\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} }\Rightarrow \\ $$$$\boldsymbol{{cos}\Psi}=\frac{\boldsymbol{{c}}}{\boldsymbol{{a}}+\boldsymbol{{b}}}\:\:\:\:\:\:\:.\:\blacksquare \\ $$

Commented by mnjuly1970 last updated on 08/Aug/22

$${grateful}\:{sir} \\ $$

Facebook Tweet Pin

Question-174666

Leave a Reply Cancel reply