Question Number 174709 by AgniMath last updated on 09/Aug/22
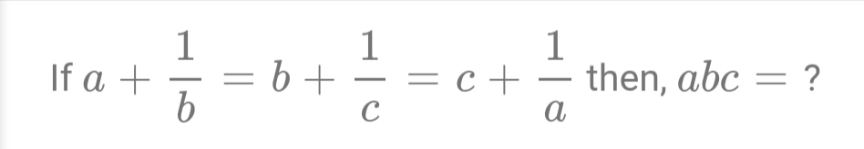
Commented by MJS_new last updated on 09/Aug/22

$$\pm\mathrm{1}? \\ $$
Commented by infinityaction last updated on 09/Aug/22
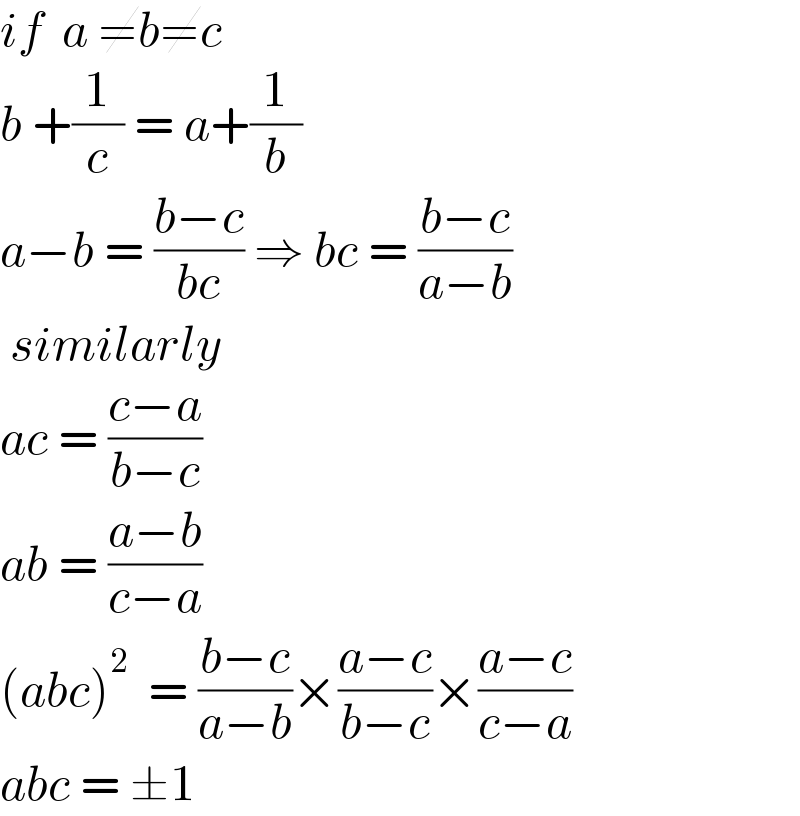
$${if}\:\:{a}\:\neq{b}\neq{c} \\ $$$${b}\:+\frac{\mathrm{1}}{{c}}\:=\:{a}+\frac{\mathrm{1}}{{b}} \\ $$$${a}−{b}\:=\:\frac{{b}−{c}}{{bc}}\:\Rightarrow\:{bc}\:=\:\frac{{b}−{c}}{{a}−{b}} \\ $$$$\:{similarly} \\ $$$${ac}\:=\:\frac{{c}−{a}}{{b}−{c}} \\ $$$${ab}\:=\:\frac{{a}−{b}}{{c}−{a}} \\ $$$$\left({abc}\right)^{\mathrm{2}} \:\:=\:\frac{{b}−{c}}{{a}−{b}}×\frac{{a}−{c}}{{b}−{c}}×\frac{{a}−{c}}{{c}−{a}} \\ $$$${abc}\:=\:\pm\mathrm{1} \\ $$
Commented by AgniMath last updated on 09/Aug/22
For answer go to:
https://math.agnibho.co.in/2022/08/q12.html
Answered by behi834171 last updated on 09/Aug/22
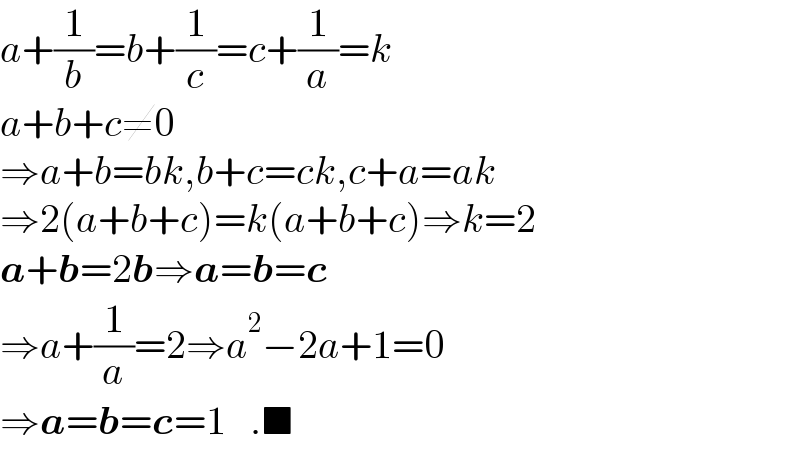
$${a}+\frac{\mathrm{1}}{{b}}={b}+\frac{\mathrm{1}}{{c}}={c}+\frac{\mathrm{1}}{{a}}={k} \\ $$$${a}+{b}+{c}\neq\mathrm{0} \\ $$$$\Rightarrow{a}+{b}={bk},{b}+{c}={ck},{c}+{a}={ak} \\ $$$$\Rightarrow\mathrm{2}\left({a}+{b}+{c}\right)={k}\left({a}+{b}+{c}\right)\Rightarrow{k}=\mathrm{2} \\ $$$$\boldsymbol{{a}}+\boldsymbol{{b}}=\mathrm{2}\boldsymbol{{b}}\Rightarrow\boldsymbol{{a}}=\boldsymbol{{b}}=\boldsymbol{{c}} \\ $$$$\Rightarrow{a}+\frac{\mathrm{1}}{{a}}=\mathrm{2}\Rightarrow{a}^{\mathrm{2}} −\mathrm{2}{a}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{{a}}=\boldsymbol{{b}}=\boldsymbol{{c}}=\mathrm{1}\:\:\:.\blacksquare \\ $$
