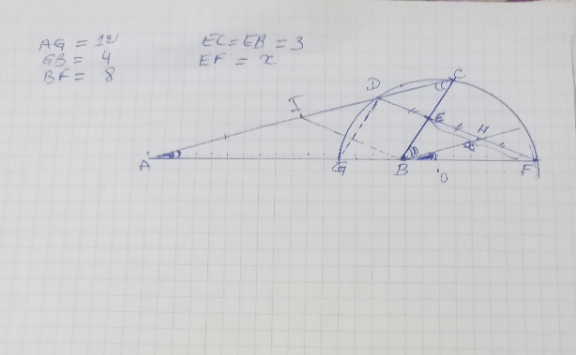
Question Number 174763 by dragan91 last updated on 10/Aug/22
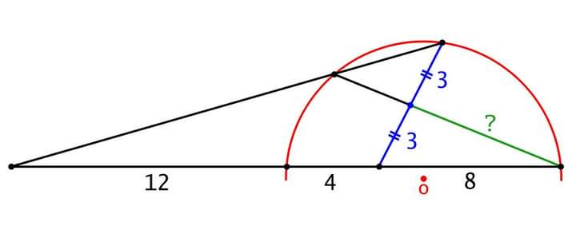
Answered by a.lgnaoui last updated on 11/Aug/22

$$\angle{ADF} \\ $$$$\frac{\mathrm{sin}\:\mathrm{A}}{\mathrm{DF}}=\frac{\mathrm{sin}\:\mathrm{F}}{\mathrm{AD}}=\frac{\mathrm{sin}\:\mathrm{D}}{\mathrm{24}}\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\angle{EBF} \\ $$$$\frac{\mathrm{sin}\:\mathrm{B}}{\mathrm{x}}=\frac{\mathrm{sin}\:\mathrm{F}}{\mathrm{3}}=\frac{\mathrm{sin}\:\mathrm{E}}{\mathrm{8}}\:\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\angle{CDE} \\ $$$$\frac{\mathrm{sin}\:\mathrm{D}}{\mathrm{3}}=\frac{\mathrm{sin}\:\mathrm{C}}{\mathrm{DE}}=\frac{\mathrm{sin}\:\mathrm{E}}{\mathrm{CD}}\:\:\:\:\:\:\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{2}\right)\:\mathrm{and}\:\left(\mathrm{3}\right) \\ $$$$\frac{\mathrm{sin}\:\mathrm{E}}{\mathrm{8}}=\frac{\mathrm{sin}\:\mathrm{F}}{\mathrm{3}}\:\:\:\mathrm{sin}\:\mathrm{E}=\mathrm{8}\frac{\mathrm{sin}\:\mathrm{F}}{\mathrm{3}} \\ $$$$\frac{\mathrm{sin}\:\mathrm{E}}{\mathrm{CD}}=\frac{\mathrm{sin}\:\mathrm{D}}{\mathrm{3}}\:\:\:\:\mathrm{sin}\:\mathrm{E}=\frac{\mathrm{CDsin}\:\mathrm{D}}{\mathrm{3}} \\ $$$$\frac{\mathrm{8sin}\:\mathrm{F}}{\mathrm{3}}=\frac{\mathrm{CDsin}\:\mathrm{D}}{\mathrm{3}}\:\:\:\mathrm{CD}=\frac{\mathrm{8sin}\:\mathrm{F}}{\mathrm{sin}\:\mathrm{D}} \\ $$$$\angle{ADF}\:\:\:\:\:\:\frac{\mathrm{sin}\:\mathrm{F}}{\mathrm{AD}}=\frac{\mathrm{sin}\:\mathrm{D}}{\mathrm{24}}\:\Rightarrow\frac{\mathrm{sin}\:\mathrm{F}}{\mathrm{sin}\:\mathrm{D}}=\frac{\mathrm{AD}}{\mathrm{24}} \\ $$$$\mathrm{CD}=\mathrm{8}\frac{\mathrm{AD}}{\mathrm{24}}\:\:\:\:,\:\:\mathrm{CD}=\frac{\mathrm{AD}}{\mathrm{3}}\:\:\Rightarrow\:\:\:\mathrm{AC}=\mathrm{4CD} \\ $$$$\frac{\mathrm{CD}}{\mathrm{CI}}=\frac{\mathrm{CE}}{\mathrm{BC}}=\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{DE}}{\mathrm{BI}}\:\:\left(\mathrm{DE}\parallel\mathrm{BI}\right) \\ $$$$\mathrm{GD}\mid\mid\mathrm{BC}\:\:\:\frac{\mathrm{FE}}{\mathrm{FD}}=\frac{\mathrm{FB}}{\mathrm{FG}}\:\:\Rightarrow\:\:\:\:\:\frac{\mathrm{x}}{\mathrm{FD}}=\frac{\mathrm{8}}{\mathrm{12}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{H}\in\mathrm{EF}\:\:\:\left(\:\:\mathrm{BH}\mid\mid\mathrm{AC}\right)\:\:\measuredangle{DCB}=\measuredangle{CBH} \\ $$$$\measuredangle{C}+\measuredangle{D}=\measuredangle{B}+\measuredangle{F}\:\:\:{CE}={BE}\Rightarrow{DE}={EH}\:\:=\mathrm{3}\:\:\:\:\measuredangle{HBF}=\measuredangle{A}\:\:{CD}={BH} \\ $$$${EF}=\mathrm{2}×\mathrm{3}=\mathrm{6}\:\:\Rightarrow\:\:\:\:\mathrm{x}=\mathrm{6} \\ $$
Commented by Tawa11 last updated on 11/Aug/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by a.lgnaoui last updated on 11/Aug/22