Question Number 174823 by ajfour last updated on 11/Aug/22
Commented by ajfour last updated on 11/Aug/22

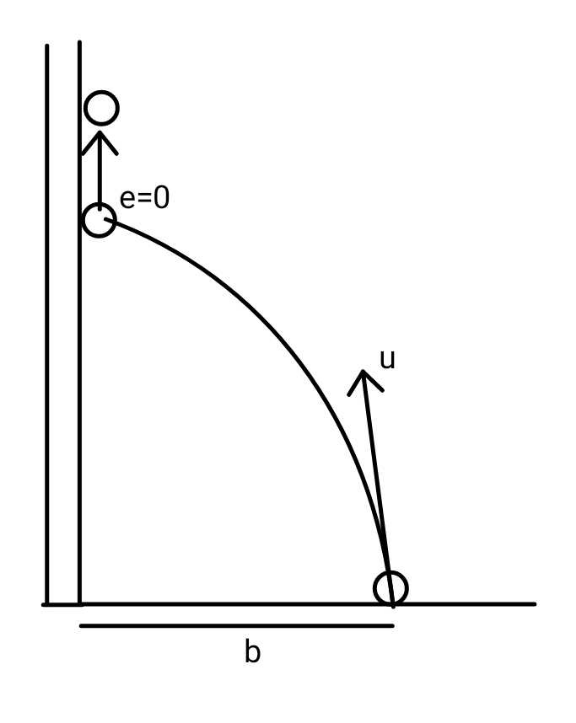
$${Find}\:{maximum}\:{height}\:{the}\:{ball} \\ $$$${can}\:{climb}\:{up}\:{the}\:{wall}. \\ $$
Answered by mr W last updated on 13/Aug/22
![t_1 =(b/(u cos θ)) v_1 =u sin θ−((gb)/(u cos θ)) ≥0 sin 2θ≥((2gb)/u^2 ) ⇒(1/2)sin^(−1) ((2gb)/u^2 )≤θ≤(π/2)−(1/2)sin^(−1) ((2gb)/u^2 ) ⇒u≥(√(2gb)) max. height reached: h=(((u sin θ)^2 )/(2g))=((u^2 (1−cos 2θ))/(4g)) ≤ (u^2 /(4g))[1+(√(1−(((2gb)/u^2 ))^2 ))]=h_(max)](https://www.tinkutara.com/question/Q174874.png)
$${t}_{\mathrm{1}} =\frac{{b}}{{u}\:\mathrm{cos}\:\theta} \\ $$$${v}_{\mathrm{1}} ={u}\:\mathrm{sin}\:\theta−\frac{{gb}}{{u}\:\mathrm{cos}\:\theta}\:\geqslant\mathrm{0} \\ $$$$\mathrm{sin}\:\mathrm{2}\theta\geqslant\frac{\mathrm{2}{gb}}{{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}{gb}}{{u}^{\mathrm{2}} }\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}{gb}}{{u}^{\mathrm{2}} } \\ $$$$\Rightarrow{u}\geqslant\sqrt{\mathrm{2}{gb}} \\ $$$${max}.\:{height}\:{reached}: \\ $$$${h}=\frac{\left({u}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{\mathrm{2}{g}}=\frac{{u}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right)}{\mathrm{4}{g}} \\ $$$$\:\:\:\leqslant\:\frac{{u}^{\mathrm{2}} }{\mathrm{4}{g}}\left[\mathrm{1}+\sqrt{\mathrm{1}−\left(\frac{\mathrm{2}{gb}}{{u}^{\mathrm{2}} }\right)^{\mathrm{2}} }\right]={h}_{{max}} \\ $$
Commented by ajfour last updated on 13/Aug/22
$${thanks}\:{sir},\:{perfect}! \\ $$
Commented by Tawa11 last updated on 14/Aug/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
