Question Number 174844 by daus last updated on 12/Aug/22

Commented by daus last updated on 12/Aug/22

$${pls}\:{help}\:{for}\:{D}\: \\ $$$${a}^{{k}} \:+\:{a}^{{k}+\mathrm{2}} \:+…..\:{n}^{{th}} \:{term} \\ $$
Answered by Rasheed.Sindhi last updated on 12/Aug/22
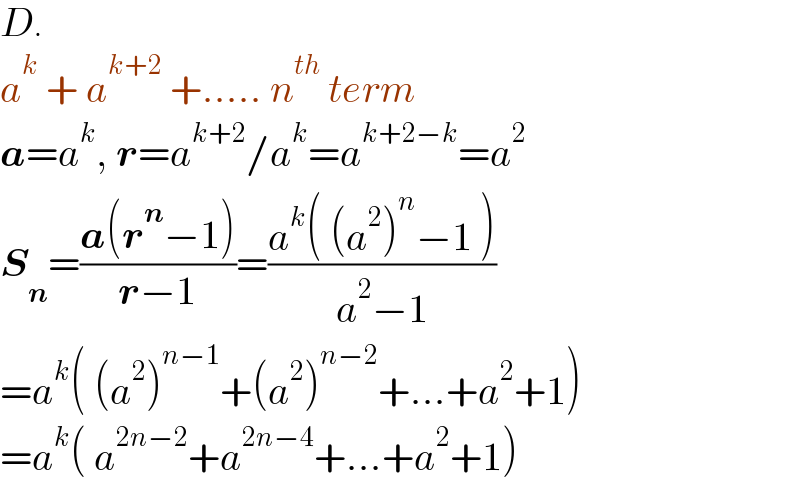
$${D}. \\ $$$${a}^{{k}} \:+\:{a}^{{k}+\mathrm{2}} \:+…..\:{n}^{{th}} \:{term} \\ $$$$\boldsymbol{{a}}={a}^{{k}} ,\:\boldsymbol{{r}}={a}^{{k}+\mathrm{2}} /{a}^{{k}} ={a}^{{k}+\mathrm{2}−{k}} ={a}^{\mathrm{2}} \\ $$$$\boldsymbol{{S}}_{\boldsymbol{{n}}} =\frac{\boldsymbol{{a}}\left(\boldsymbol{{r}}^{\boldsymbol{{n}}} −\mathrm{1}\right)}{\boldsymbol{{r}}−\mathrm{1}}=\frac{{a}^{{k}} \left(\:\left({a}^{\mathrm{2}} \right)^{{n}} −\mathrm{1}\:\right)}{{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$$={a}^{{k}} \left(\:\left({a}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} +\left({a}^{\mathrm{2}} \right)^{{n}−\mathrm{2}} +…+{a}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$={a}^{{k}} \left(\:{a}^{\mathrm{2}{n}−\mathrm{2}} +{a}^{\mathrm{2}{n}−\mathrm{4}} +…+{a}^{\mathrm{2}} +\mathrm{1}\right) \\ $$
Commented by daus last updated on 13/Aug/22
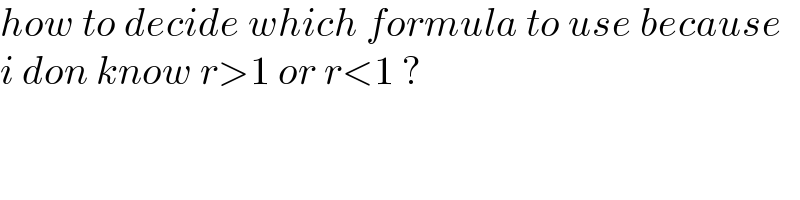
$${how}\:{to}\:{decide}\:{which}\:{formula}\:{to}\:{use}\:{because}\: \\ $$$${i}\:{don}\:{know}\:{r}>\mathrm{1}\:{or}\:{r}<\mathrm{1}\:? \\ $$
