Question Number 174863 by cortano1 last updated on 13/Aug/22
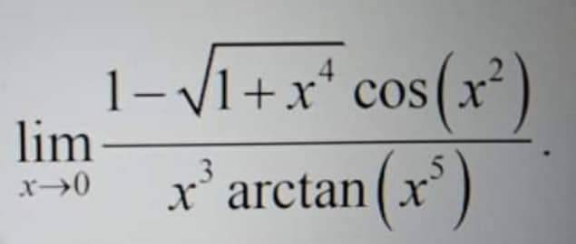
Commented by kaivan.ahmadi last updated on 13/Aug/22
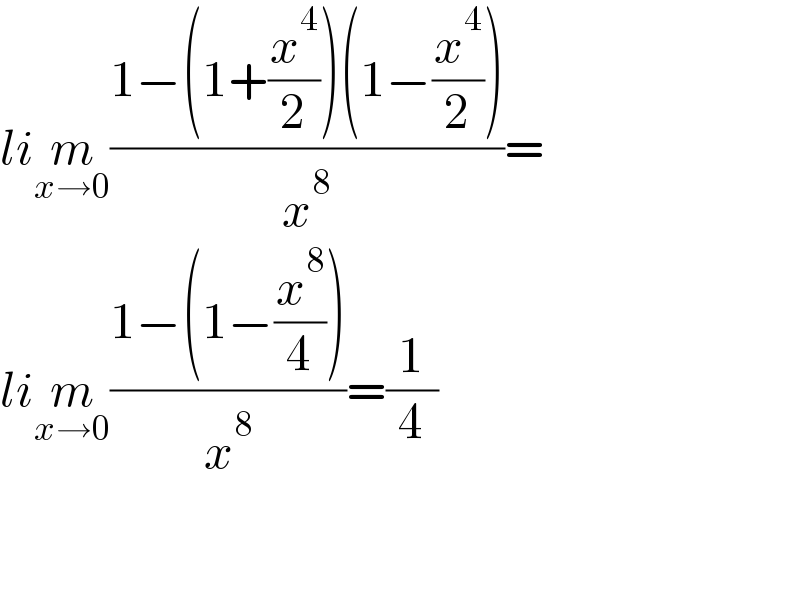
$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{\mathrm{1}−\left(\mathrm{1}+\frac{{x}^{\mathrm{4}} }{\mathrm{2}}\right)\left(\mathrm{1}−\frac{{x}^{\mathrm{4}} }{\mathrm{2}}\right)}{{x}^{\mathrm{8}} }= \\ $$$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{\mathrm{1}−\left(\mathrm{1}−\frac{{x}^{\mathrm{8}} }{\mathrm{4}}\right)}{{x}^{\mathrm{8}} }=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$
Commented by cortano1 last updated on 13/Aug/22

$${no} \\ $$
Commented by cortano1 last updated on 13/Aug/22
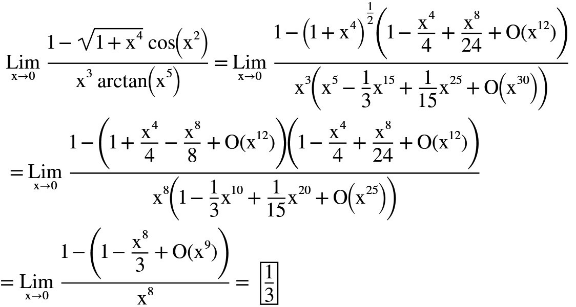
Answered by blackmamba last updated on 13/Aug/22
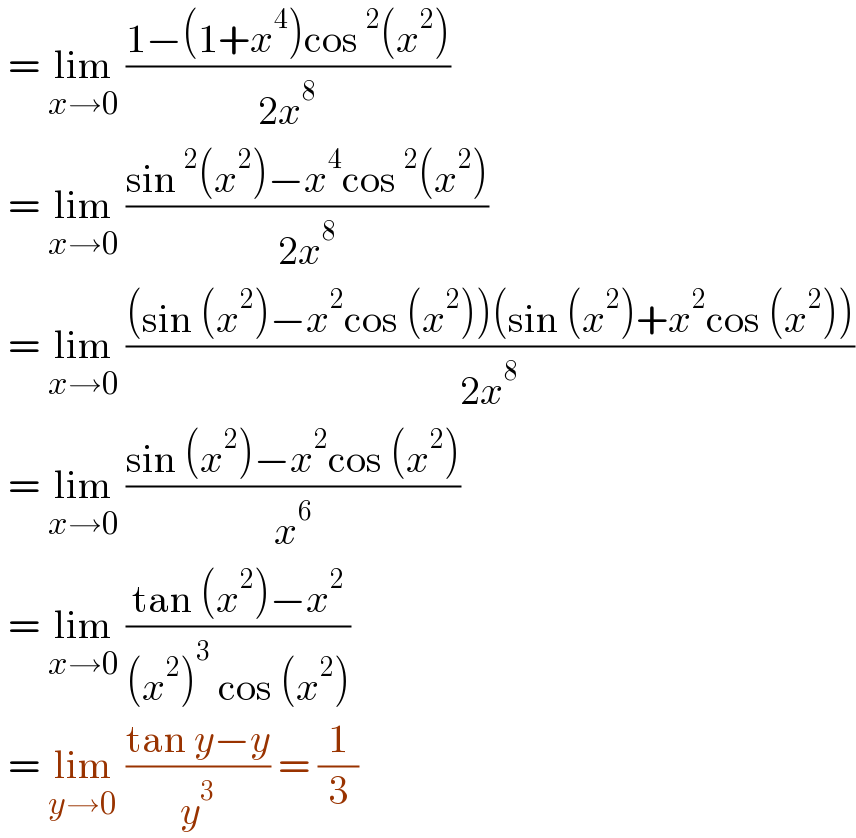
$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}+{x}^{\mathrm{4}} \right)\mathrm{cos}\:^{\mathrm{2}} \left({x}^{\mathrm{2}} \right)}{\mathrm{2}{x}^{\mathrm{8}} } \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:^{\mathrm{2}} \left({x}^{\mathrm{2}} \right)−{x}^{\mathrm{4}} \mathrm{cos}\:^{\mathrm{2}} \left({x}^{\mathrm{2}} \right)}{\mathrm{2}{x}^{\mathrm{8}} } \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{sin}\:\left({x}^{\mathrm{2}} \right)−{x}^{\mathrm{2}} \mathrm{cos}\:\left({x}^{\mathrm{2}} \right)\right)\left(\mathrm{sin}\:\left({x}^{\mathrm{2}} \right)+{x}^{\mathrm{2}} \mathrm{cos}\:\left({x}^{\mathrm{2}} \right)\right)}{\mathrm{2}{x}^{\mathrm{8}} } \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left({x}^{\mathrm{2}} \right)−{x}^{\mathrm{2}} \mathrm{cos}\:\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{6}} } \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left({x}^{\mathrm{2}} \right)−{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \right)^{\mathrm{3}} \:\mathrm{cos}\:\left({x}^{\mathrm{2}} \right)} \\ $$$$\:=\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:{y}−{y}}{{y}^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$
