Question Number 174902 by daus last updated on 14/Aug/22

Answered by Ar Brandon last updated on 14/Aug/22
![∫_0 ^4 (1/((1+(√x))^2 ))dx , x=t^2 ⇒dx=2tdt =∫_0 ^2 ((2t)/((1+t)^2 ))dt=2∫_0 ^2 ((1/(1+t))−(1/((1+t)^2 )))dt =2[ln(1+t)+(1/(1+t))]_0 ^2 =2(ln3+(1/3)−1) =2(ln3−(2/3))=ln9−(4/3)](https://www.tinkutara.com/question/Q174906.png)
$$\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\mathrm{1}}{\left(\mathrm{1}+\sqrt{{x}}\right)^{\mathrm{2}} }{dx}\:,\:{x}={t}^{\mathrm{2}} \:\Rightarrow{dx}=\mathrm{2}{tdt} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{2}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{1}+{t}}−\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\right){dt} \\ $$$$\:\:\:\:=\mathrm{2}\left[\mathrm{ln}\left(\mathrm{1}+{t}\right)+\frac{\mathrm{1}}{\mathrm{1}+{t}}\right]_{\mathrm{0}} ^{\mathrm{2}} =\mathrm{2}\left(\mathrm{ln3}+\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}\right) \\ $$$$\:\:\:\:=\mathrm{2}\left(\mathrm{ln3}−\frac{\mathrm{2}}{\mathrm{3}}\right)=\mathrm{ln9}−\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by floor(10²Eta[1]) last updated on 14/Aug/22

$$\mathrm{it}'\mathrm{s}\:\mathrm{2}\left(\mathrm{ln3}+\frac{\mathrm{1}}{\mathrm{3}}\right)−\mathrm{2} \\ $$
Commented by Ar Brandon last updated on 14/Aug/22
Yes, you're right. Thanks!
Commented by daus last updated on 14/Aug/22
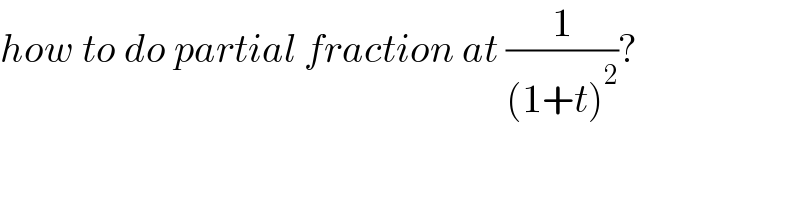
$${how}\:{to}\:{do}\:{partial}\:{fraction}\:{at}\:\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }? \\ $$
Commented by Ar Brandon last updated on 14/Aug/22
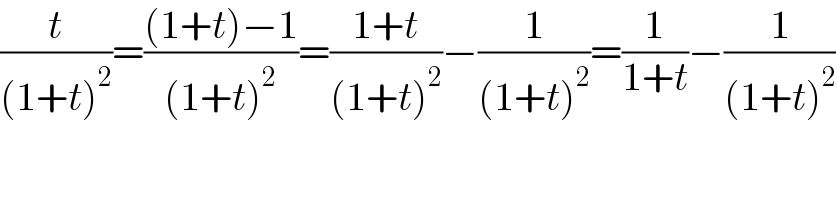
$$\frac{{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }=\frac{\left(\mathrm{1}+{t}\right)−\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }=\frac{\mathrm{1}+{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{1}+{t}}−\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} } \\ $$
