Menu Close

Question-174933

Tinku Tara 0 Comments
Pin




Question Number 174933 by AgniMath last updated on 14/Aug/22
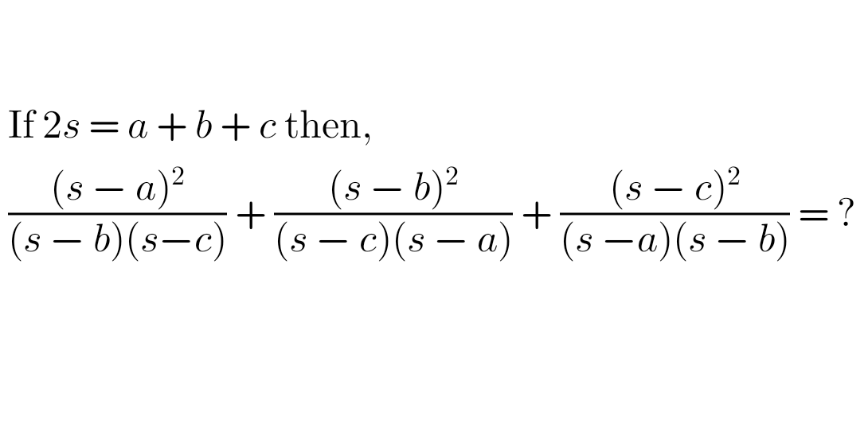
Answered by Rasheed.Sindhi last updated on 15/Aug/22
A=(((s−a)^2 )/((s−b)(s−c)))+(((s−b)^2 )/((s−a)(s−c)))+(((s−c)^2 )/((s−a)(s−b))) 2s=a+b+c, t=ab+bc+ca (say) A=(((s−a)^3 +(s−b)^3 +(s−c)^3 )/((s−a)(s−b)(s−c)))−3+3 =(((s−a)^3 +(s−b)^3 +(s−c)^3 −3(s−a)(s−b)(s−c)_(N) )/((s−a)(s−b)(s−c)_(D) ))+3 A=(N/D)+3 N=( (s−a)+(s−b)+(s−c)_(I) )((s−a)^2 +(s−b)^2 +(s−c)^2 _(II) −((s−a)(s−b)+(s−b)(s−c)+(s−a)(s−c)_(III) ) I=3s−(a+b+c)=3s−2s=s II=3s^2 +a^2 +b^2 +c^2 −2s(a+b+c) =3s^2 +(a+b+c)^2 −2(ab+bc+ca)−2s(2s) =3s^2 +(2s)^2 −2(t)−4s^2 =3s^2 −2t III=3s^2 +ab+bc+ca−2s(a+b+c) =3s^2 +t−4s^2 =−s^2 +t N=(s)( 3s^2 −2t−(−s^2 +t) ) =s(4s^2 −3t)=4s^3 −3st D=s^3 −s^2 (a+b+c)+s(ab+bc+ca)−abc =s^3 −s^2 (2s)+s(t)−abc =−s^3 +st−abc A=(N/D)+3⇒A=((4s^3 −3st)/(−s^3 +st−abc))+3 A=((4s^3 −3st−3s^3 +3st−3abc)/(−s^3 +st−abc)) =((s^3 −3abc)/(−s^3 +st−abc)) =(((((a+b+c)/2))^3 −3abc)/(−(((a+b+c)/2))^3 +(((a+b+c)/2))(ab+bc+ca)−abc)) A=(((a+b+c)^3 −24abc)/(−(a+b+c)^3 +4(a+b+c)(ab+bc+ca)−8abc))
$${A}=\frac{\left({s}−{a}\right)^{\mathrm{2}} }{\left({s}−{b}\right)\left({s}−{c}\right)}+\frac{\left({s}−{b}\right)^{\mathrm{2}} }{\left({s}−{a}\right)\left({s}−{c}\right)}+\frac{\left({s}−{c}\right)^{\mathrm{2}} }{\left({s}−{a}\right)\left({s}−{b}\right)} \\ $$$$\mathrm{2}{s}={a}+{b}+{c},\:\:\:\:\:{t}={ab}+{bc}+{ca}\:\left({say}\right) \\ $$$${A}=\frac{\left({s}−{a}\right)^{\mathrm{3}} +\left({s}−{b}\right)^{\mathrm{3}} +\left({s}−{c}\right)^{\mathrm{3}} }{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}−\mathrm{3}+\mathrm{3} \\ $$$$\:=\frac{\underset{{N}} {\underbrace{\left({s}−{a}\right)^{\mathrm{3}} +\left({s}−{b}\right)^{\mathrm{3}} +\left({s}−{c}\right)^{\mathrm{3}} −\mathrm{3}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}}}{\underset{{D}} {\underbrace{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}}}+\mathrm{3} \\ $$$${A}=\frac{{N}}{{D}}+\mathrm{3} \\ $$$${N}=\left(\:\left(\underset{\mathrm{I}} {\underbrace{{s}−{a}\right)+\left({s}−{b}\right)+\left({s}−{c}\right)}}\:\right)\left(\left(\underset{\mathrm{II}} {\underbrace{{s}−{a}\right)^{\mathrm{2}} +\left({s}−{b}\right)^{\mathrm{2}} +\left({s}−{c}\right)^{\mathrm{2}} }}−\left(\underset{\mathrm{III}} {\underbrace{\left({s}−{a}\right)\left({s}−{b}\right)+\left({s}−{b}\right)\left({s}−{c}\right)+\left({s}−{a}\right)\left({s}−{c}\right)}}\:\right)\right. \\ $$$$\mathrm{I}=\mathrm{3}{s}−\left({a}+{b}+{c}\right)=\mathrm{3}{s}−\mathrm{2}{s}={s} \\ $$$$\mathrm{II}=\mathrm{3}{s}^{\mathrm{2}} +{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{s}\left({a}+{b}+{c}\right) \\ $$$$\:\:\:=\mathrm{3}{s}^{\mathrm{2}} +\left({a}+{b}+{c}\right)^{\mathrm{2}} −\mathrm{2}\left({ab}+{bc}+{ca}\right)−\mathrm{2}{s}\left(\mathrm{2}{s}\right) \\ $$$$\:\:\:=\mathrm{3}{s}^{\mathrm{2}} +\cancel{\left(\mathrm{2}{s}\right)^{\mathrm{2}} }−\mathrm{2}\left({t}\right)−\cancel{\mathrm{4}{s}^{\mathrm{2}} } \\ $$$$\:\:\:=\mathrm{3}{s}^{\mathrm{2}} −\mathrm{2}{t} \\ $$$$\mathrm{III}=\mathrm{3}{s}^{\mathrm{2}} +{ab}+{bc}+{ca}−\mathrm{2}{s}\left({a}+{b}+{c}\right) \\ $$$$\:\:\:\:\:=\mathrm{3}{s}^{\mathrm{2}} +{t}−\mathrm{4}{s}^{\mathrm{2}} =−{s}^{\mathrm{2}} +{t} \\ $$$${N}=\left({s}\right)\left(\:\mathrm{3}{s}^{\mathrm{2}} −\mathrm{2}{t}−\left(−{s}^{\mathrm{2}} +{t}\right)\:\right) \\ $$$$\:\:\:\:\:={s}\left(\mathrm{4}{s}^{\mathrm{2}} −\mathrm{3}{t}\right)=\mathrm{4}{s}^{\mathrm{3}} −\mathrm{3}{st} \\ $$$$ \\ $$$${D}={s}^{\mathrm{3}} −{s}^{\mathrm{2}} \left({a}+{b}+{c}\right)+{s}\left({ab}+{bc}+{ca}\right)−{abc} \\ $$$$\:\:\:\:={s}^{\mathrm{3}} −{s}^{\mathrm{2}} \left(\mathrm{2}{s}\right)+{s}\left({t}\right)−{abc} \\ $$$$\:\:\:\:=−{s}^{\mathrm{3}} +{st}−{abc} \\ $$$$ \\ $$$${A}=\frac{{N}}{{D}}+\mathrm{3}\Rightarrow{A}=\frac{\mathrm{4}{s}^{\mathrm{3}} −\mathrm{3}{st}}{−{s}^{\mathrm{3}} +{st}−{abc}}+\mathrm{3} \\ $$$${A}=\frac{\mathrm{4}{s}^{\mathrm{3}} −\mathrm{3}{st}−\mathrm{3}{s}^{\mathrm{3}} +\mathrm{3}{st}−\mathrm{3}{abc}}{−{s}^{\mathrm{3}} +{st}−{abc}} \\ $$$$\:\:\:=\frac{{s}^{\mathrm{3}} −\mathrm{3}{abc}}{−{s}^{\mathrm{3}} +{st}−{abc}} \\ $$$$\:\:=\frac{\left(\frac{{a}+{b}+{c}}{\mathrm{2}}\right)^{\mathrm{3}} −\mathrm{3}{abc}}{−\left(\frac{{a}+{b}+{c}}{\mathrm{2}}\right)^{\mathrm{3}} +\left(\frac{{a}+{b}+{c}}{\mathrm{2}}\right)\left({ab}+{bc}+{ca}\right)−{abc}} \\ $$$${A}=\frac{\left({a}+{b}+{c}\right)^{\mathrm{3}} −\mathrm{24}{abc}}{−\left({a}+{b}+{c}\right)^{\mathrm{3}} +\mathrm{4}\left({a}+{b}+{c}\right)\left({ab}+{bc}+{ca}\right)−\mathrm{8}{abc}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *