Question Number 174975 by sciencestudent last updated on 15/Aug/22

Answered by MikeH last updated on 15/Aug/22
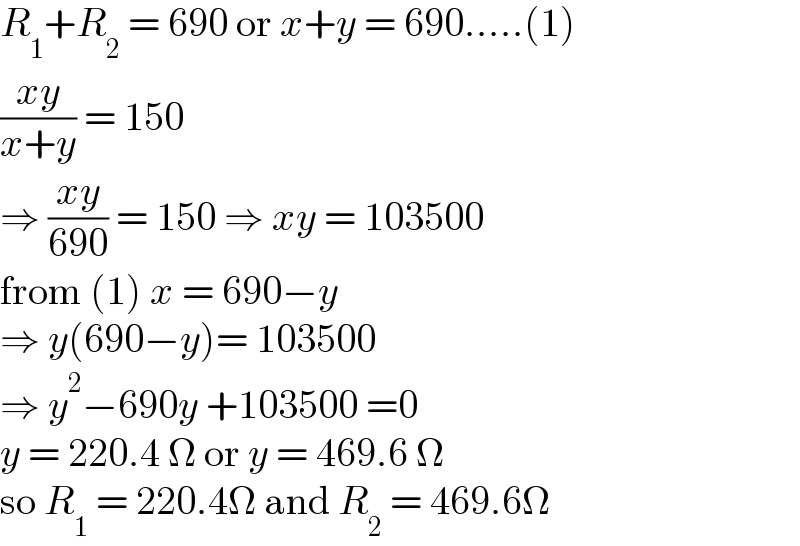
$${R}_{\mathrm{1}} +{R}_{\mathrm{2}} \:=\:\mathrm{690}\:\mathrm{or}\:{x}+{y}\:=\:\mathrm{690}…..\left(\mathrm{1}\right) \\ $$$$\frac{{xy}}{{x}+{y}}\:=\:\mathrm{150} \\ $$$$\Rightarrow\:\frac{{xy}}{\mathrm{690}}\:=\:\mathrm{150}\:\Rightarrow\:{xy}\:=\:\mathrm{103500}\: \\ $$$$\mathrm{from}\:\left(\mathrm{1}\right)\:{x}\:=\:\mathrm{690}−{y} \\ $$$$\Rightarrow\:{y}\left(\mathrm{690}−{y}\right)=\:\mathrm{103500} \\ $$$$\Rightarrow\:{y}^{\mathrm{2}} −\mathrm{690}{y}\:+\mathrm{103500}\:=\mathrm{0} \\ $$$${y}\:=\:\mathrm{220}.\mathrm{4}\:\Omega\:\mathrm{or}\:{y}\:=\:\mathrm{469}.\mathrm{6}\:\Omega \\ $$$$\mathrm{so}\:{R}_{\mathrm{1}} \:=\:\mathrm{220}.\mathrm{4}\Omega\:\mathrm{and}\:{R}_{\mathrm{2}} \:=\:\mathrm{469}.\mathrm{6}\Omega \\ $$
