Question-175000

Question Number 175000 by mr W last updated on 15/Aug/22

Commented by mr W last updated on 16/Aug/22

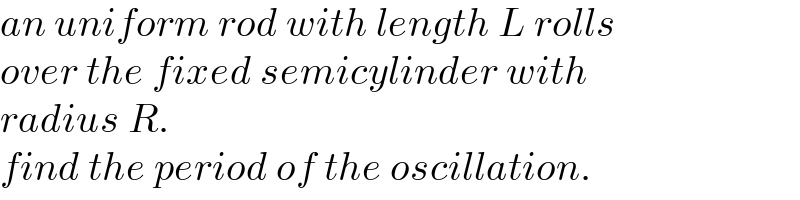
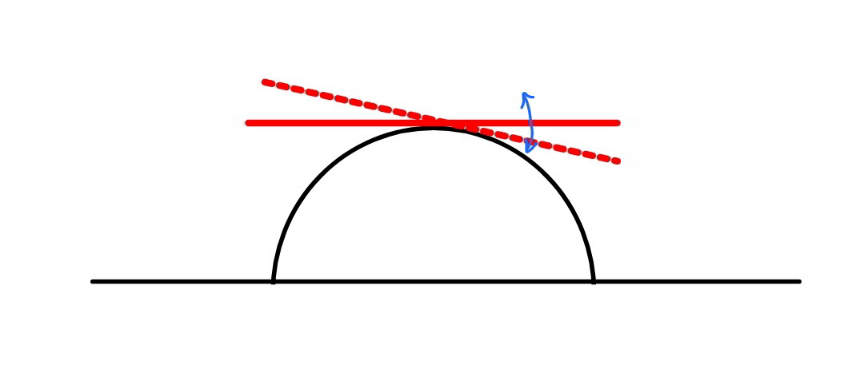
$${an}\:{uniform}\:{rod}\:{with}\:{length}\:{L}\:{rolls} \\ $$$${over}\:{the}\:{fixed}\:{semicylinder}\:{with}\: \\ $$$${radius}\:{R}. \\ $$$${find}\:{the}\:{period}\:{of}\:{the}\:{oscillation}. \\ $$

Answered by mr W last updated on 16/Aug/22

Commented by ajfour last updated on 16/Aug/22

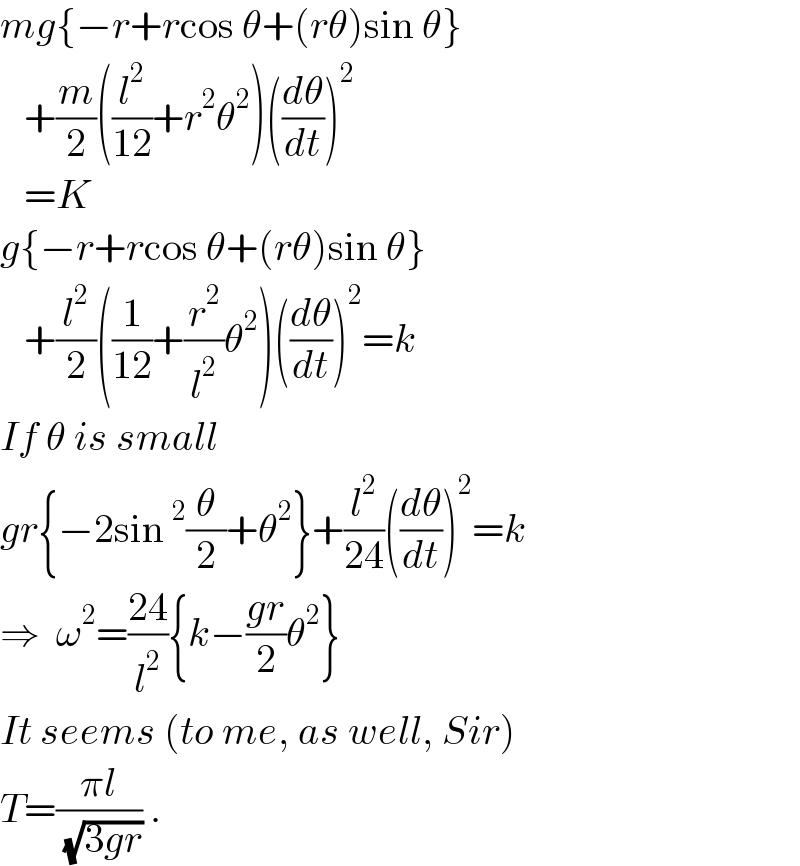
mg{−r+rcos θ+(rθ)sin θ} +(m/2)((l^2 /(12))+r^2 θ^2 )((dθ/dt))^2 =K g{−r+rcos θ+(rθ)sin θ} +(l^2 /2)((1/(12))+(r^2 /l^2 )θ^2 )((dθ/dt))^2 =k If θ is small gr{−2sin^2 (θ/2)+θ^2 }+(l^2 /(24))((dθ/dt))^2 =k ⇒ ω^2 =((24)/l^2 ){k−((gr)/2)θ^2 } It seems (to me, as well, Sir) T=((πl)/( (√(3gr)))) .

$${mg}\left\{−{r}+{r}\mathrm{cos}\:\theta+\left({r}\theta\right)\mathrm{sin}\:\theta\right\} \\ $$$$\:\:\:+\frac{{m}}{\mathrm{2}}\left(\frac{{l}^{\mathrm{2}} }{\mathrm{12}}+{r}^{\mathrm{2}} \theta^{\mathrm{2}} \right)\left(\frac{{d}\theta}{{dt}}\right)^{\mathrm{2}} \\ $$$$\:\:\:={K} \\ $$$${g}\left\{−{r}+{r}\mathrm{cos}\:\theta+\left({r}\theta\right)\mathrm{sin}\:\theta\right\} \\ $$$$\:\:\:+\frac{{l}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{12}}+\frac{{r}^{\mathrm{2}} }{{l}^{\mathrm{2}} }\theta^{\mathrm{2}} \right)\left(\frac{{d}\theta}{{dt}}\right)^{\mathrm{2}} ={k} \\ $$$${If}\:\theta\:{is}\:{small} \\ $$$${gr}\left\{−\mathrm{2sin}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}+\theta^{\mathrm{2}} \right\}+\frac{{l}^{\mathrm{2}} }{\mathrm{24}}\left(\frac{{d}\theta}{{dt}}\right)^{\mathrm{2}} ={k} \\ $$$$\Rightarrow\:\:\omega^{\mathrm{2}} =\frac{\mathrm{24}}{{l}^{\mathrm{2}} }\left\{{k}−\frac{{gr}}{\mathrm{2}}\theta^{\mathrm{2}} \right\} \\ $$$${It}\:{seems}\:\left({to}\:{me},\:{as}\:{well},\:{Sir}\right) \\ $$$${T}=\frac{\pi{l}}{\:\sqrt{\mathrm{3}{gr}}}\:. \\ $$

Commented by mr W last updated on 16/Aug/22

MC=Rθ I_C =((L^2 m)/(12))+m(Rθ)^2 (d/dt)(I_C (dθ/dt))=−mg(Rθ)cos θ [((L^2 m)/(12))+m(Rθ)^2 ](d^2 θ/dt^2 )+2mR^2 θ((dθ/dt))^2 =−mg(Rθ)cos θ [(L^2 /(12))+(Rθ)^2 ](d^2 θ/dt^2 )=−Rθ[g cos θ+2R((dθ/dt))^2 ] for very small θ, we can say ≈ (L^2 /(12))×(d^2 θ/dt^2 )=−gRθ ⇒(d^2 θ/dt^2 )+((12gR)/L^2 )θ=0 ω=(√((12gR)/L^2 )) ⇒T=((2π)/ω)=((πL)/( (√(3gR))))

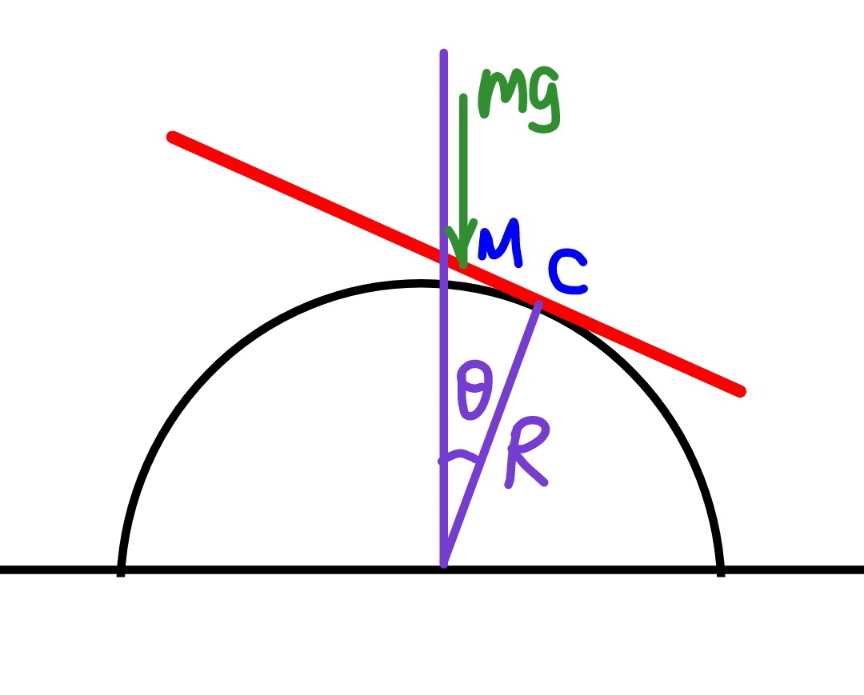
$${MC}={R}\theta \\ $$$${I}_{{C}} =\frac{{L}^{\mathrm{2}} {m}}{\mathrm{12}}+{m}\left({R}\theta\right)^{\mathrm{2}} \\ $$$$\frac{{d}}{{dt}}\left({I}_{{C}} \frac{{d}\theta}{{dt}}\right)=−{mg}\left({R}\theta\right)\mathrm{cos}\:\theta \\ $$$$\left[\frac{{L}^{\mathrm{2}} {m}}{\mathrm{12}}+{m}\left({R}\theta\right)^{\mathrm{2}} \right]\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }+\mathrm{2}{mR}^{\mathrm{2}} \theta\left(\frac{{d}\theta}{{dt}}\right)^{\mathrm{2}} =−{mg}\left({R}\theta\right)\mathrm{cos}\:\theta \\ $$$$\left[\frac{{L}^{\mathrm{2}} }{\mathrm{12}}+\left({R}\theta\right)^{\mathrm{2}} \right]\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }=−{R}\theta\left[{g}\:\mathrm{cos}\:\theta+\mathrm{2}{R}\left(\frac{{d}\theta}{{dt}}\right)^{\mathrm{2}} \right] \\ $$$${for}\:{very}\:{small}\:\theta,\:{we}\:{can}\:{say} \\ $$$$\approx\:\:\frac{{L}^{\mathrm{2}} }{\mathrm{12}}×\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }=−{gR}\theta \\ $$$$\Rightarrow\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }+\frac{\mathrm{12}{gR}}{{L}^{\mathrm{2}} }\theta=\mathrm{0} \\ $$$$\omega=\sqrt{\frac{\mathrm{12}{gR}}{{L}^{\mathrm{2}} }} \\ $$$$\Rightarrow{T}=\frac{\mathrm{2}\pi}{\omega}=\frac{\pi{L}}{\:\sqrt{\mathrm{3}{gR}}} \\ $$

Commented by mr W last updated on 17/Aug/22

$${yes}\:{sir},\:{thanks}! \\ $$

Commented by Tawa11 last updated on 17/Aug/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply