Question Number 175059 by mr W last updated on 17/Aug/22
Commented by mr W last updated on 17/Aug/22
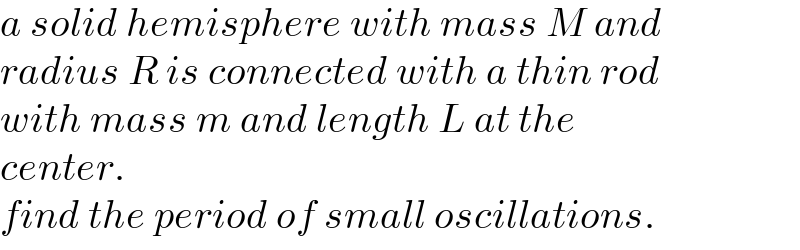
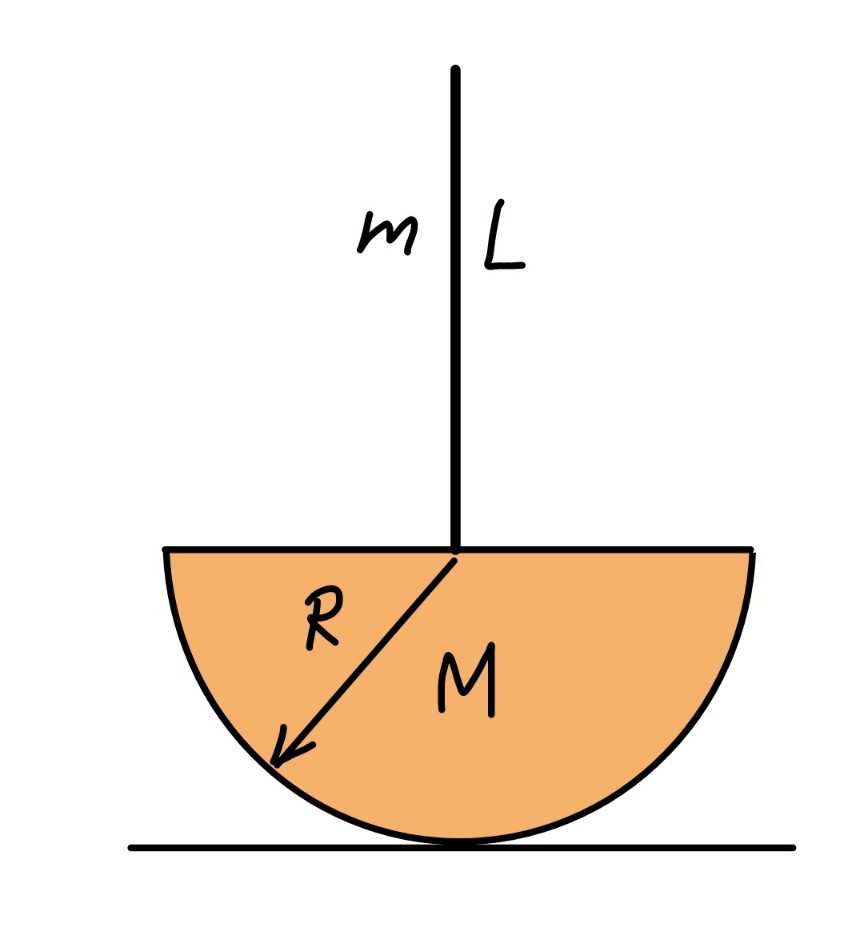
$${a}\:{solid}\:{hemisphere}\:{with}\:{mass}\:{M}\:{and} \\ $$$${radius}\:{R}\:{is}\:{connected}\:{with}\:{a}\:{thin}\:{rod}\: \\ $$$${with}\:{mass}\:{m}\:{and}\:{length}\:{L}\:{at}\:{the}\: \\ $$$${center}. \\ $$$${find}\:{the}\:{period}\:{of}\:{small}\:{oscillations}. \\ $$
Commented by mr W last updated on 18/Aug/22

Answered by mr W last updated on 18/Aug/22

Commented by mr W last updated on 18/Aug/22

$${OA}=\frac{{L}}{\mathrm{2}} \\ $$$${OB}=\frac{\mathrm{3}{R}}{\mathrm{8}} \\ $$$${e}={OC} \\ $$$${e}+\frac{{L}}{\mathrm{2}}=\frac{{M}}{{m}+{M}}×\left(\frac{{L}}{\mathrm{2}}+\frac{\mathrm{3}{R}}{\mathrm{8}}\right) \\ $$$${e}=\frac{{M}}{{m}+{M}}×\left(\frac{{L}}{\mathrm{2}}+\frac{\mathrm{3}{R}}{\mathrm{8}}\right)−\frac{{L}}{\mathrm{2}}>\mathrm{0} \\ $$$${I}_{{P}} =\frac{{mL}^{\mathrm{2}} }{\mathrm{12}}+{m}\left({R}+\frac{{L}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{83}{MR}^{\mathrm{2}} }{\mathrm{320}}+{M}\left(\frac{\mathrm{5}{R}}{\mathrm{8}}\right)^{\mathrm{2}} \\ $$$${I}_{{P}} ={m}\left(\frac{{L}^{\mathrm{2}} }{\mathrm{3}}+{R}^{\mathrm{2}} +{RL}\right)+\frac{\mathrm{13}{MR}^{\mathrm{2}} }{\mathrm{20}} \\ $$
Commented by mr W last updated on 18/Aug/22

Commented by mr W last updated on 18/Aug/22
![I_p ((dθ/dt))^2 +(m+M)g(R−e cos θ)=E=constant 2I_p ((dθ/dt))(d^2 θ/dt^2 )+(m+M)ge sin θ (dθ/dt)=0 2I_p (d^2 θ/dt^2 )+(m+M)ge sin θ=0 for small θ, sin θ≈θ ⇒(d^2 θ/dt^2 )+(((m+M)eg)/(2I_P ))θ=0 → d.e. of s.h.m. ω=(√(((m+M)eg)/(2I_P )))=(1/2)(√(([4(M−m)L+3MR]g)/(2m((L^2 /3)+R^2 +RL)+((13MR^2 )/(10))))) T=((2π)/ω)=4π(√((20m((L^2 /3)+R^2 +RL)+13MR^2 )/(10[4(M−m)L+3MR]g)))](https://www.tinkutara.com/question/Q175094.png)
$${I}_{{p}} \left(\frac{{d}\theta}{{dt}}\right)^{\mathrm{2}} +\left({m}+{M}\right){g}\left({R}−{e}\:\mathrm{cos}\:\theta\right)={E}={constant} \\ $$$$\mathrm{2}{I}_{{p}} \left(\frac{{d}\theta}{{dt}}\right)\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }+\left({m}+{M}\right){ge}\:\mathrm{sin}\:\theta\:\frac{{d}\theta}{{dt}}=\mathrm{0} \\ $$$$\mathrm{2}{I}_{{p}} \frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }+\left({m}+{M}\right){ge}\:\mathrm{sin}\:\theta=\mathrm{0} \\ $$$${for}\:{small}\:\theta,\:\mathrm{sin}\:\theta\approx\theta \\ $$$$\Rightarrow\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }+\frac{\left({m}+{M}\right){eg}}{\mathrm{2}{I}_{{P}} }\theta=\mathrm{0}\:\:\:\:\rightarrow\:{d}.{e}.\:{of}\:{s}.{h}.{m}. \\ $$$$\omega=\sqrt{\frac{\left({m}+{M}\right){eg}}{\mathrm{2}{I}_{{P}} }}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left[\mathrm{4}\left({M}−{m}\right){L}+\mathrm{3}{MR}\right]{g}}{\mathrm{2}{m}\left(\frac{{L}^{\mathrm{2}} }{\mathrm{3}}+{R}^{\mathrm{2}} +{RL}\right)+\frac{\mathrm{13}{MR}^{\mathrm{2}} }{\mathrm{10}}}} \\ $$$${T}=\frac{\mathrm{2}\pi}{\omega}=\mathrm{4}\pi\sqrt{\frac{\mathrm{20}{m}\left(\frac{{L}^{\mathrm{2}} }{\mathrm{3}}+{R}^{\mathrm{2}} +{RL}\right)+\mathrm{13}{MR}^{\mathrm{2}} }{\mathrm{10}\left[\mathrm{4}\left({M}−{m}\right){L}+\mathrm{3}{MR}\right]{g}}} \\ $$
Commented by Tawa11 last updated on 20/Aug/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
