Menu Close

Question-175066

Tinku Tara 0 Comments
Pin




Question Number 175066 by peter frank last updated on 17/Aug/22
Answered by mr W last updated on 17/Aug/22
Commented by mr W last updated on 17/Aug/22
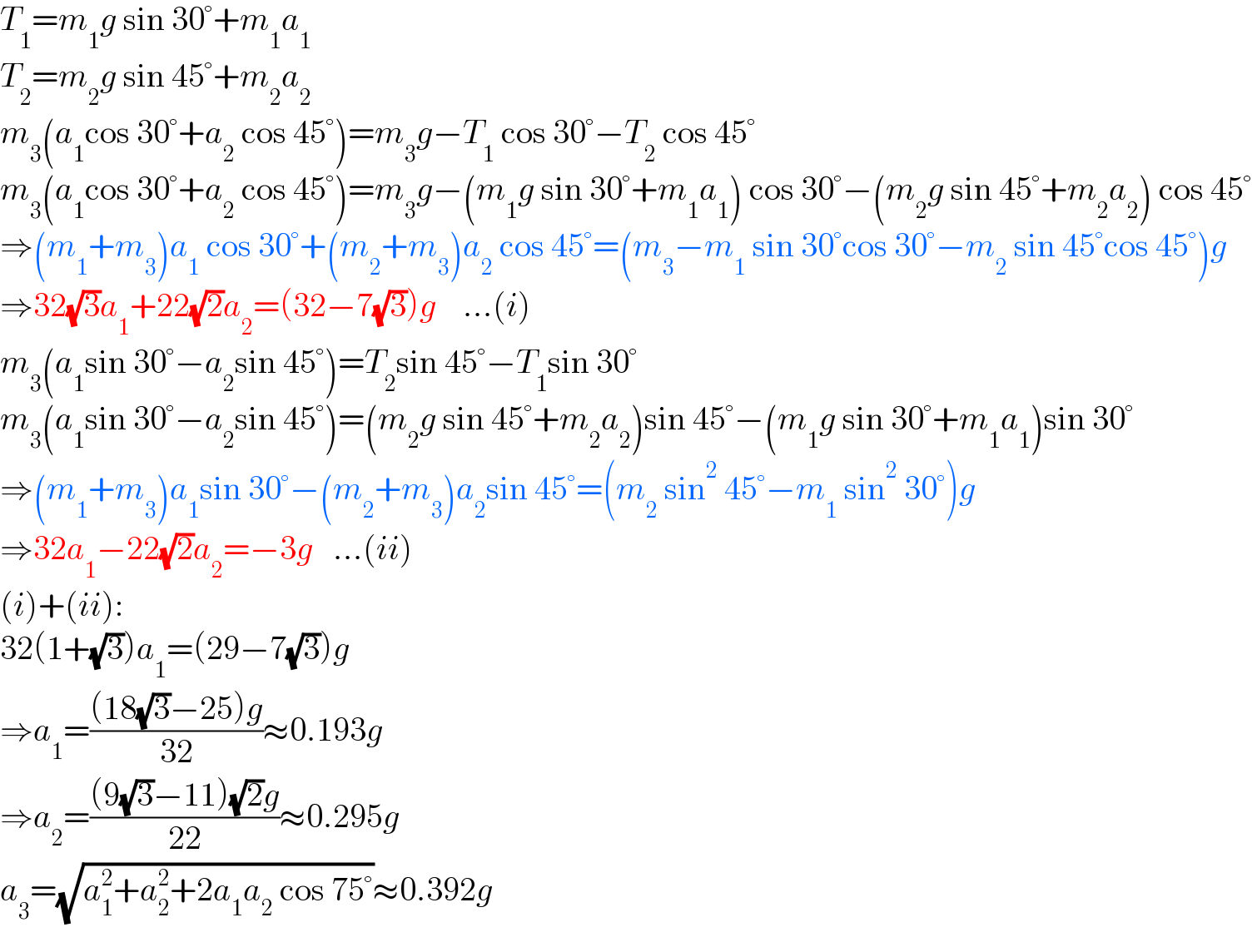
T_1 =m_1 g sin 30°+m_1 a_1 T_2 =m_2 g sin 45°+m_2 a_2 m_3 (a_1 cos 30°+a_2 cos 45°)=m_3 g−T_1 cos 30°−T_2 cos 45° m_3 (a_1 cos 30°+a_2 cos 45°)=m_3 g−(m_1 g sin 30°+m_1 a_1 ) cos 30°−(m_2 g sin 45°+m_2 a_2 ) cos 45° ⇒(m_1 +m_3 )a_1 cos 30°+(m_2 +m_3 )a_2 cos 45°=(m_3 −m_1 sin 30°cos 30°−m_2 sin 45°cos 45°)g ⇒32(√3)a_1 +22(√2)a_2 =(32−7(√3))g ...(i) m_3 (a_1 sin 30°−a_2 sin 45°)=T_2 sin 45°−T_1 sin 30° m_3 (a_1 sin 30°−a_2 sin 45°)=(m_2 g sin 45°+m_2 a_2 )sin 45°−(m_1 g sin 30°+m_1 a_1 )sin 30° ⇒(m_1 +m_3 )a_1 sin 30°−(m_2 +m_3 )a_2 sin 45°=(m_2 sin^2 45°−m_1 sin^2 30°)g ⇒32a_1 −22(√2)a_2 =−3g ...(ii) (i)+(ii): 32(1+(√3))a_1 =(29−7(√3))g ⇒a_1 =(((18(√3)−25)g)/(32))≈0.193g ⇒a_2 =(((9(√3)−11)(√2)g)/(22))≈0.295g a_3 =(√(a_1 ^2 +a_2 ^2 +2a_1 a_2 cos 75°))≈0.392g
$${T}_{\mathrm{1}} ={m}_{\mathrm{1}} {g}\:\mathrm{sin}\:\mathrm{30}°+{m}_{\mathrm{1}} {a}_{\mathrm{1}} \\ $$$${T}_{\mathrm{2}} ={m}_{\mathrm{2}} {g}\:\mathrm{sin}\:\mathrm{45}°+{m}_{\mathrm{2}} {a}_{\mathrm{2}} \\ $$$${m}_{\mathrm{3}} \left({a}_{\mathrm{1}} \mathrm{cos}\:\mathrm{30}°+{a}_{\mathrm{2}} \:\mathrm{cos}\:\mathrm{45}°\right)={m}_{\mathrm{3}} {g}−{T}_{\mathrm{1}} \:\mathrm{cos}\:\mathrm{30}°−{T}_{\mathrm{2}} \:\mathrm{cos}\:\mathrm{45}° \\ $$$${m}_{\mathrm{3}} \left({a}_{\mathrm{1}} \mathrm{cos}\:\mathrm{30}°+{a}_{\mathrm{2}} \:\mathrm{cos}\:\mathrm{45}°\right)={m}_{\mathrm{3}} {g}−\left({m}_{\mathrm{1}} {g}\:\mathrm{sin}\:\mathrm{30}°+{m}_{\mathrm{1}} {a}_{\mathrm{1}} \right)\:\mathrm{cos}\:\mathrm{30}°−\left({m}_{\mathrm{2}} {g}\:\mathrm{sin}\:\mathrm{45}°+{m}_{\mathrm{2}} {a}_{\mathrm{2}} \right)\:\mathrm{cos}\:\mathrm{45}° \\ $$$$\Rightarrow\left({m}_{\mathrm{1}} +{m}_{\mathrm{3}} \right){a}_{\mathrm{1}} \:\mathrm{cos}\:\mathrm{30}°+\left({m}_{\mathrm{2}} +{m}_{\mathrm{3}} \right){a}_{\mathrm{2}} \:\mathrm{cos}\:\mathrm{45}°=\left({m}_{\mathrm{3}} −{m}_{\mathrm{1}} \:\mathrm{sin}\:\mathrm{30}°\mathrm{cos}\:\mathrm{30}°−{m}_{\mathrm{2}} \:\mathrm{sin}\:\mathrm{45}°\mathrm{cos}\:\mathrm{45}°\right){g} \\ $$$$\Rightarrow\mathrm{32}\sqrt{\mathrm{3}}{a}_{\mathrm{1}} +\mathrm{22}\sqrt{\mathrm{2}}{a}_{\mathrm{2}} =\left(\mathrm{32}−\mathrm{7}\sqrt{\mathrm{3}}\right){g}\:\:\:\:…\left({i}\right) \\ $$$${m}_{\mathrm{3}} \left({a}_{\mathrm{1}} \mathrm{sin}\:\mathrm{30}°−{a}_{\mathrm{2}} \mathrm{sin}\:\mathrm{45}°\right)={T}_{\mathrm{2}} \mathrm{sin}\:\mathrm{45}°−{T}_{\mathrm{1}} \mathrm{sin}\:\mathrm{30}° \\ $$$${m}_{\mathrm{3}} \left({a}_{\mathrm{1}} \mathrm{sin}\:\mathrm{30}°−{a}_{\mathrm{2}} \mathrm{sin}\:\mathrm{45}°\right)=\left({m}_{\mathrm{2}} {g}\:\mathrm{sin}\:\mathrm{45}°+{m}_{\mathrm{2}} {a}_{\mathrm{2}} \right)\mathrm{sin}\:\mathrm{45}°−\left({m}_{\mathrm{1}} {g}\:\mathrm{sin}\:\mathrm{30}°+{m}_{\mathrm{1}} {a}_{\mathrm{1}} \right)\mathrm{sin}\:\mathrm{30}° \\ $$$$\Rightarrow\left({m}_{\mathrm{1}} +{m}_{\mathrm{3}} \right){a}_{\mathrm{1}} \mathrm{sin}\:\mathrm{30}°−\left({m}_{\mathrm{2}} +{m}_{\mathrm{3}} \right){a}_{\mathrm{2}} \mathrm{sin}\:\mathrm{45}°=\left({m}_{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\mathrm{45}°−{m}_{\mathrm{1}} \:\mathrm{sin}^{\mathrm{2}} \:\mathrm{30}°\right){g} \\ $$$$\Rightarrow\mathrm{32}{a}_{\mathrm{1}} −\mathrm{22}\sqrt{\mathrm{2}}{a}_{\mathrm{2}} =−\mathrm{3}{g}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$$\mathrm{32}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){a}_{\mathrm{1}} =\left(\mathrm{29}−\mathrm{7}\sqrt{\mathrm{3}}\right){g} \\ $$$$\Rightarrow{a}_{\mathrm{1}} =\frac{\left(\mathrm{18}\sqrt{\mathrm{3}}−\mathrm{25}\right){g}}{\mathrm{32}}\approx\mathrm{0}.\mathrm{193}{g} \\ $$$$\Rightarrow{a}_{\mathrm{2}} =\frac{\left(\mathrm{9}\sqrt{\mathrm{3}}−\mathrm{11}\right)\sqrt{\mathrm{2}}{g}}{\mathrm{22}}\approx\mathrm{0}.\mathrm{295}{g} \\ $$$${a}_{\mathrm{3}} =\sqrt{{a}_{\mathrm{1}} ^{\mathrm{2}} +{a}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{a}_{\mathrm{1}} {a}_{\mathrm{2}} \:\mathrm{cos}\:\mathrm{75}°}\approx\mathrm{0}.\mathrm{392}{g} \\ $$
Commented by Tawa11 last updated on 17/Aug/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by peter frank last updated on 18/Aug/22
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *