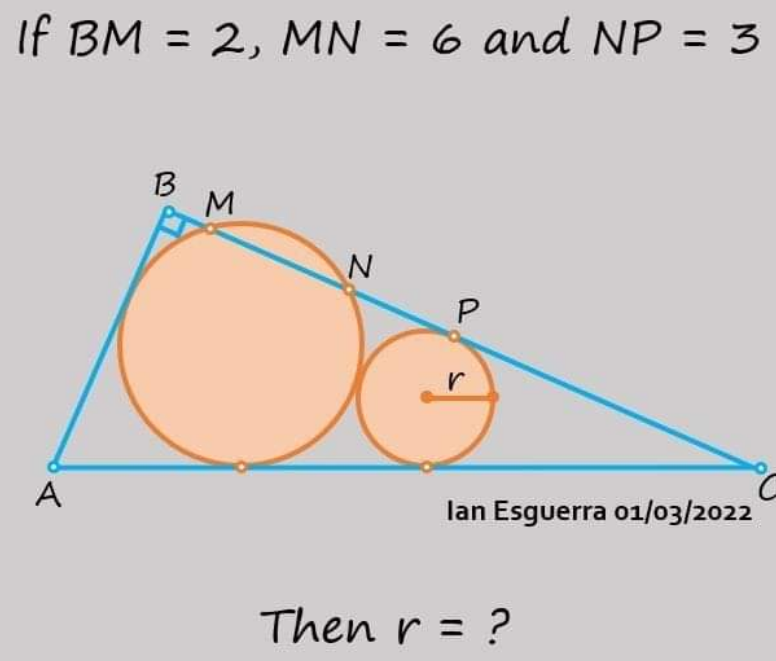
Question Number 175199 by cherokeesay last updated on 22/Aug/22
Answered by som(math1967) last updated on 23/Aug/22
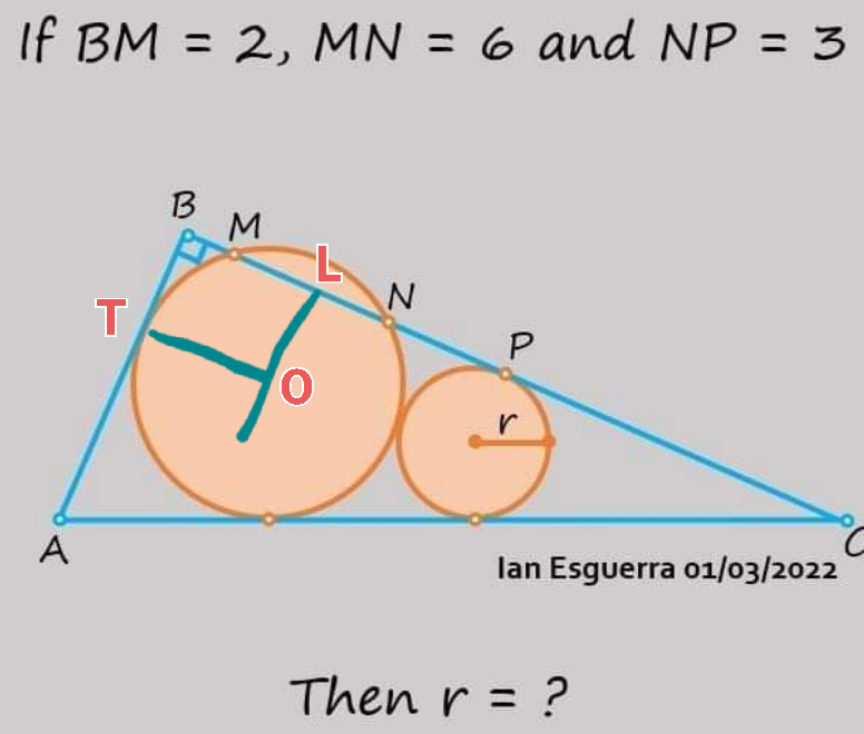
Commented by som(math1967) last updated on 23/Aug/22
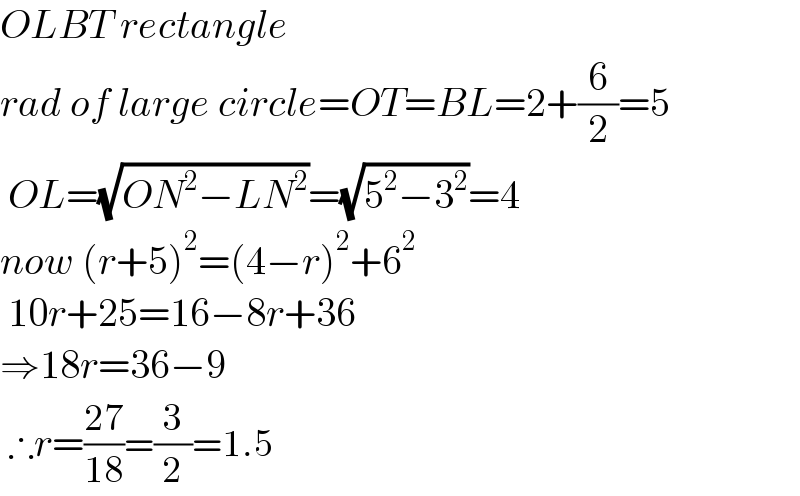
$${OLBT}\:{rectangle} \\ $$$${rad}\:{of}\:{large}\:{circle}={OT}={BL}=\mathrm{2}+\frac{\mathrm{6}}{\mathrm{2}}=\mathrm{5} \\ $$$$\:{OL}=\sqrt{{ON}^{\mathrm{2}} −{LN}^{\mathrm{2}} }=\sqrt{\mathrm{5}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }=\mathrm{4} \\ $$$${now}\:\left({r}+\mathrm{5}\right)^{\mathrm{2}} =\left(\mathrm{4}−{r}\right)^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} \\ $$$$\:\mathrm{10}{r}+\mathrm{25}=\mathrm{16}−\mathrm{8}{r}+\mathrm{36} \\ $$$$\Rightarrow\mathrm{18}{r}=\mathrm{36}−\mathrm{9} \\ $$$$\:\therefore{r}=\frac{\mathrm{27}}{\mathrm{18}}=\frac{\mathrm{3}}{\mathrm{2}}=\mathrm{1}.\mathrm{5} \\ $$
Commented by cherokeesay last updated on 23/Aug/22

$${perfect} \\ $$$${thank}\:{you}\:{sir}. \\ $$
Commented by Tawa11 last updated on 23/Aug/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
