Question Number 175230 by infinityaction last updated on 24/Aug/22

Answered by Ar Brandon last updated on 24/Aug/22
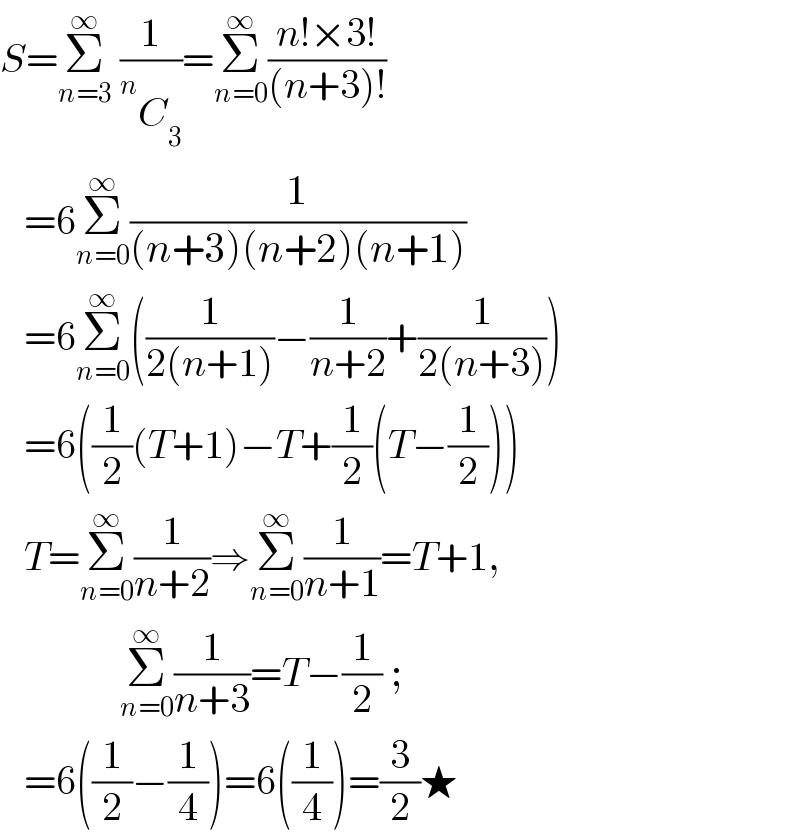
$${S}=\underset{{n}=\mathrm{3}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\overset{{n}} {\:}{C}_{\mathrm{3}} }=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}!×\mathrm{3}!}{\left({n}+\mathrm{3}\right)!} \\ $$$$\:\:\:=\mathrm{6}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{3}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right)} \\ $$$$\:\:\:=\mathrm{6}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{n}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{3}\right)}\right) \\ $$$$\:\:\:=\mathrm{6}\left(\frac{\mathrm{1}}{\mathrm{2}}\left({T}+\mathrm{1}\right)−{T}+\frac{\mathrm{1}}{\mathrm{2}}\left({T}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:{T}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{2}}\Rightarrow\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{1}}={T}+\mathrm{1}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{3}}={T}−\frac{\mathrm{1}}{\mathrm{2}}\:; \\ $$$$\:\:\:=\mathrm{6}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right)=\mathrm{6}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\frac{\mathrm{3}}{\mathrm{2}}\bigstar \\ $$
Commented by infinityaction last updated on 24/Aug/22
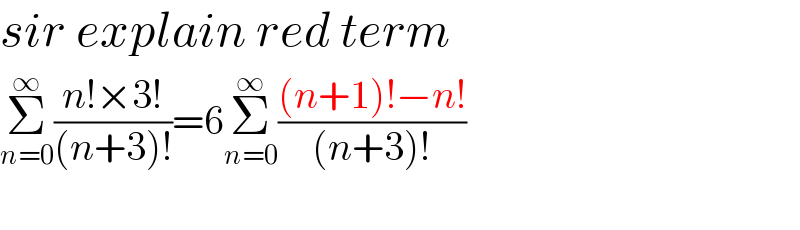
$${sir}\:{explain}\:{red}\:{term} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}!×\mathrm{3}!}{\left({n}+\mathrm{3}\right)!}=\mathrm{6}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({n}+\mathrm{1}\right)!−{n}!}{\left({n}+\mathrm{3}\right)!} \\ $$$$\:\:\: \\ $$
Commented by infinityaction last updated on 24/Aug/22
$${okey}\:{sir}\:{thank}\:{you} \\ $$
Commented by Ar Brandon last updated on 24/Aug/22
Sorry, mistake. Edited!
Commented by Tawa11 last updated on 25/Aug/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
