Question Number 175264 by Beginner last updated on 25/Aug/22

Answered by Rasheed.Sindhi last updated on 25/Aug/22
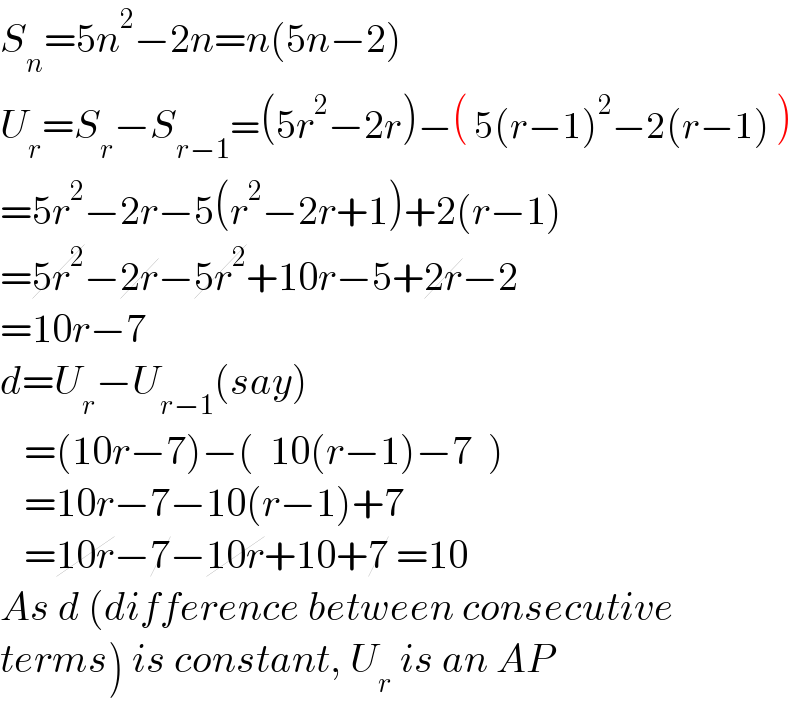
$${S}_{{n}} =\mathrm{5}{n}^{\mathrm{2}} −\mathrm{2}{n}={n}\left(\mathrm{5}{n}−\mathrm{2}\right) \\ $$$${U}_{{r}} ={S}_{{r}} −{S}_{{r}−\mathrm{1}} =\left(\mathrm{5}{r}^{\mathrm{2}} −\mathrm{2}{r}\right)−\left(\:\mathrm{5}\left({r}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left({r}−\mathrm{1}\right)\:\right) \\ $$$$=\mathrm{5}{r}^{\mathrm{2}} −\mathrm{2}{r}−\mathrm{5}\left({r}^{\mathrm{2}} −\mathrm{2}{r}+\mathrm{1}\right)+\mathrm{2}\left({r}−\mathrm{1}\right) \\ $$$$=\cancel{\mathrm{5}{r}^{\mathrm{2}} }−\cancel{\mathrm{2}{r}}−\cancel{\mathrm{5}{r}^{\mathrm{2}} }+\mathrm{10}{r}−\mathrm{5}+\cancel{\mathrm{2}{r}}−\mathrm{2} \\ $$$$=\mathrm{10}{r}−\mathrm{7} \\ $$$${d}={U}_{{r}} −{U}_{{r}−\mathrm{1}} \left({say}\right) \\ $$$$\:\:\:=\left(\mathrm{10}{r}−\mathrm{7}\right)−\left(\:\:\mathrm{10}\left({r}−\mathrm{1}\right)−\mathrm{7}\:\:\right) \\ $$$$\:\:\:=\mathrm{10}{r}−\mathrm{7}−\mathrm{10}\left({r}−\mathrm{1}\right)+\mathrm{7}\: \\ $$$$\:\:\:=\cancel{\mathrm{10}{r}}−\cancel{\mathrm{7}}−\cancel{\mathrm{10}{r}}+\mathrm{10}+\cancel{\mathrm{7}}\:=\mathrm{10} \\ $$$${As}\:{d}\:\left({difference}\:{between}\:{consecutive}\right. \\ $$$$\left.{terms}\right)\:{is}\:{constant},\:{U}_{{r}} \:{is}\:{an}\:{AP}\: \\ $$
