Question Number 175275 by mnjuly1970 last updated on 25/Aug/22
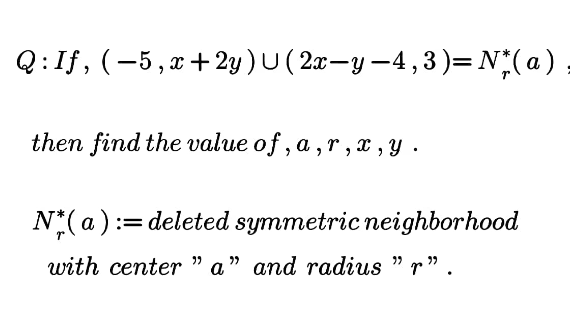
Answered by Rasheed.Sindhi last updated on 25/Aug/22
![(−5, x+2y)∪(2x−y−4, 3) =(−5,a)∪(a,3) a=x+2y=2x−y−4=((−5+3)/2)=−1 a=−1 x+2y=−1 ∧ 2x−y−4=−1 x=1, y=−1 (−5, −1)∪(−1, 3) r=∣−1−(−5)∣=4 [ or r=∣−1−3∣=4 ] a=−1, r=4 x=1, y=−1](https://www.tinkutara.com/question/Q175278.png)
$$\left(−\mathrm{5},\:{x}+\mathrm{2}{y}\right)\cup\left(\mathrm{2}{x}−{y}−\mathrm{4},\:\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(−\mathrm{5},{a}\right)\cup\left({a},\mathrm{3}\right) \\ $$$${a}={x}+\mathrm{2}{y}=\mathrm{2}{x}−{y}−\mathrm{4}=\frac{−\mathrm{5}+\mathrm{3}}{\mathrm{2}}=−\mathrm{1} \\ $$$${a}=−\mathrm{1} \\ $$$${x}+\mathrm{2}{y}=−\mathrm{1}\:\wedge\:\mathrm{2}{x}−{y}−\mathrm{4}=−\mathrm{1} \\ $$$${x}=\mathrm{1},\:{y}=−\mathrm{1} \\ $$$$ \\ $$$$\left(−\mathrm{5},\:−\mathrm{1}\right)\cup\left(−\mathrm{1},\:\mathrm{3}\right) \\ $$$${r}=\mid−\mathrm{1}−\left(−\mathrm{5}\right)\mid=\mathrm{4} \\ $$$$\left[\:{or}\:\:\:{r}=\mid−\mathrm{1}−\mathrm{3}\mid=\mathrm{4}\:\right] \\ $$$${a}=−\mathrm{1},\:{r}=\mathrm{4} \\ $$$${x}=\mathrm{1},\:\:{y}=−\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 26/Aug/22
$$\:\:\:\:{tayeballah}\:\:{grateful}\:{sir} \\ $$
