Question Number 175396 by Shrinava last updated on 29/Aug/22

Answered by mahdipoor last updated on 29/Aug/22
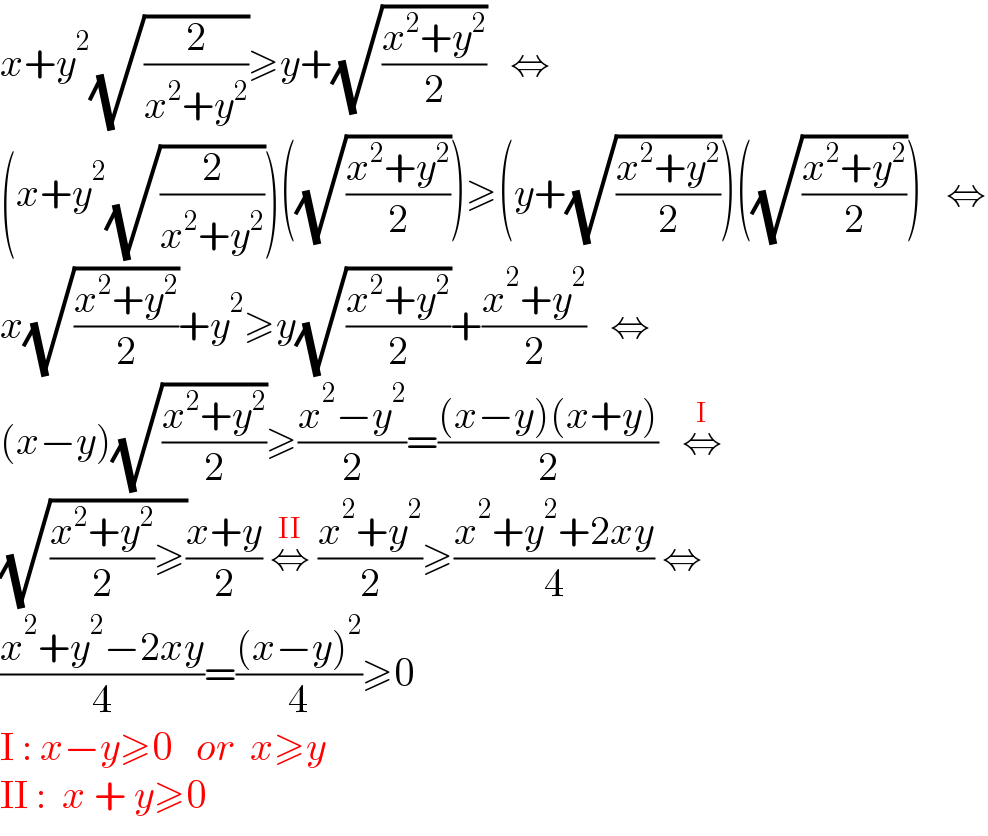
$${x}+{y}^{\mathrm{2}} \sqrt{\frac{\mathrm{2}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\geqslant{y}+\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}}\:\:\:\Leftrightarrow \\ $$$$\left({x}+{y}^{\mathrm{2}} \sqrt{\frac{\mathrm{2}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\right)\left(\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}}\right)\geqslant\left({y}+\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}}\right)\left(\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}}\right)\:\:\:\Leftrightarrow \\ $$$${x}\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}}+{y}^{\mathrm{2}} \geqslant{y}\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}}+\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}\:\:\:\Leftrightarrow \\ $$$$\left({x}−{y}\right)\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}}\geqslant\frac{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{\mathrm{2}}=\frac{\left({x}−{y}\right)\left({x}+{y}\right)}{\mathrm{2}}\:\:\:\overset{\mathrm{I}} {\Leftrightarrow} \\ $$$$\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}\geqslant}\frac{{x}+{y}}{\mathrm{2}}\:\overset{\mathrm{II}} {\Leftrightarrow}\:\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}\geqslant\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{xy}}{\mathrm{4}}\:\Leftrightarrow \\ $$$$\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{xy}}{\mathrm{4}}=\frac{\left({x}−{y}\right)^{\mathrm{2}} }{\mathrm{4}}\geqslant\mathrm{0}\:\: \\ $$$$\mathrm{I}\::\:{x}−{y}\geqslant\mathrm{0}\:\:\:{or}\:\:{x}\geqslant{y} \\ $$$$\mathrm{II}\::\:\:{x}\:+\:{y}\geqslant\mathrm{0}\:\: \\ $$
Answered by MJS_new last updated on 29/Aug/22
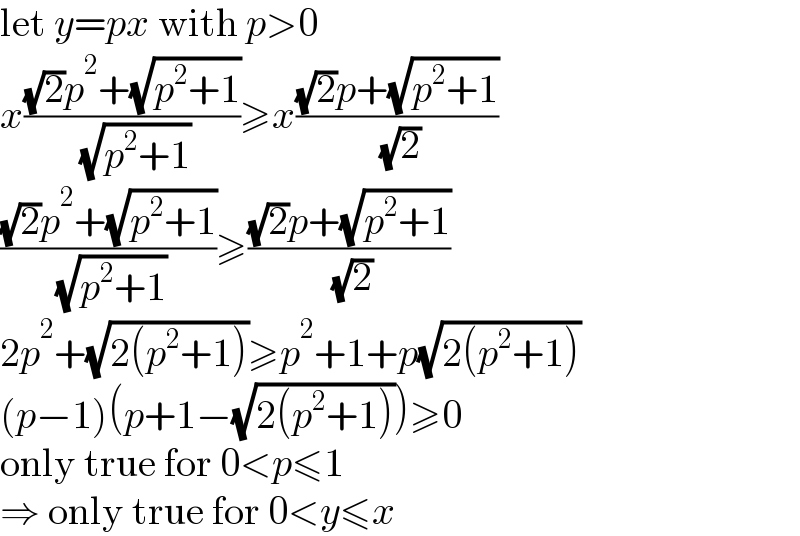
$$\mathrm{let}\:{y}={px}\:\mathrm{with}\:{p}>\mathrm{0} \\ $$$${x}\frac{\sqrt{\mathrm{2}}{p}^{\mathrm{2}} +\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}\geqslant{x}\frac{\sqrt{\mathrm{2}}{p}+\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt{\mathrm{2}}} \\ $$$$\frac{\sqrt{\mathrm{2}}{p}^{\mathrm{2}} +\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}\geqslant\frac{\sqrt{\mathrm{2}}{p}+\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{2}{p}^{\mathrm{2}} +\sqrt{\mathrm{2}\left({p}^{\mathrm{2}} +\mathrm{1}\right)}\geqslant{p}^{\mathrm{2}} +\mathrm{1}+{p}\sqrt{\mathrm{2}\left({p}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\left({p}−\mathrm{1}\right)\left({p}+\mathrm{1}−\sqrt{\mathrm{2}\left({p}^{\mathrm{2}} +\mathrm{1}\right)}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{only}\:\mathrm{true}\:\mathrm{for}\:\mathrm{0}<{p}\leqslant\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{only}\:\mathrm{true}\:\mathrm{for}\:\mathrm{0}<{y}\leqslant{x} \\ $$
