Question Number 175471 by mnjuly1970 last updated on 31/Aug/22
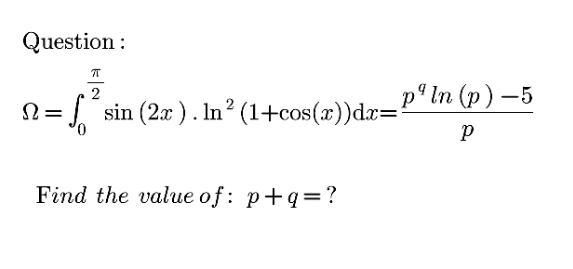
Answered by Ar Brandon last updated on 31/Aug/22
![Ω=∫_0 ^(π/2) sin2xln^2 (1+cosx)dx=2∫_0 ^(π/2) sinxcosxln^2 (1+cosx)dx =2∫_0 ^1 tln^2 (1+t)dt=[t^2 ln^2 (1+t)]_0 ^1 −2∫_0 ^1 ((t^2 ln(1+t))/(1+t))dt =ln^2 (2)−2∫_0 ^1 (t−1+(1/(1+t)))ln(1+t)dt =ln^2 (2)−2∫_0 ^1 (t−1)ln(1+t)dt−2∫_0 ^1 ((ln(1+t))/(1+t))dt =ln^2 (2)−2[((t^2 /2)−t)ln(1+t)]_0 ^1 +∫_0 ^1 ((t^2 −2t)/(t+1))dt−[ln^2 (1+t)]_0 ^1 =ln^2 (2)+ln2+∫_0 ^1 (t−3+(3/(t+1)))dt−ln^2 (2) =ln2+[(t^2 /2)−3t+3ln(t+1)]_0 ^1 =ln2−(5/2)+3ln2 =((8ln2−5)/2)=((2^3 ln2−5)/2) , ⇒p+q=2+3=5](https://www.tinkutara.com/question/Q175508.png)
$$\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin2}{x}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}{x}\right){dx}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}{x}\mathrm{cos}{x}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}{x}\right){dx} \\ $$$$\:\:\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {t}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+{t}\right){dt}=\left[{t}^{\mathrm{2}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+{t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{1}+{t}\right)}{\mathrm{1}+{t}}{dt} \\ $$$$\:\:\:\:=\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left({t}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+{t}}\right)\mathrm{ln}\left(\mathrm{1}+{t}\right){dt} \\ $$$$\:\:\:\:=\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left({t}−\mathrm{1}\right)\mathrm{ln}\left(\mathrm{1}+{t}\right){dt}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{t}\right)}{\mathrm{1}+{t}}{dt} \\ $$$$\:\:\:\:=\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{2}\left[\left(\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−{t}\right)\mathrm{ln}\left(\mathrm{1}+{t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{2}} −\mathrm{2}{t}}{{t}+\mathrm{1}}{dt}−\left[\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+{t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:=\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\mathrm{ln2}+\int_{\mathrm{0}} ^{\mathrm{1}} \left({t}−\mathrm{3}+\frac{\mathrm{3}}{{t}+\mathrm{1}}\right){dt}−\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$$\:\:\:\:=\mathrm{ln2}+\left[\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{3}{t}+\mathrm{3ln}\left({t}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{ln2}−\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{3ln2} \\ $$$$\:\:\:\:=\frac{\mathrm{8ln2}−\mathrm{5}}{\mathrm{2}}=\frac{\mathrm{2}^{\mathrm{3}} \mathrm{ln2}−\mathrm{5}}{\mathrm{2}}\:,\:\Rightarrow{p}+{q}=\mathrm{2}+\mathrm{3}=\mathrm{5} \\ $$
Commented by mnjuly1970 last updated on 31/Aug/22

$${thanks}\:{alot}\:{sir}… \\ $$
Commented by Ar Brandon last updated on 31/Aug/22
You're welcome, Sir !
