Question Number 175553 by BHOOPENDRA last updated on 02/Sep/22
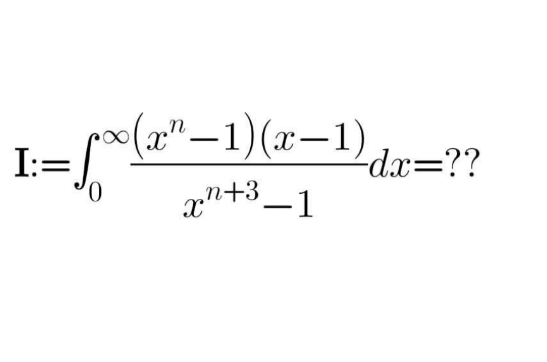
Answered by Frix last updated on 03/Sep/22
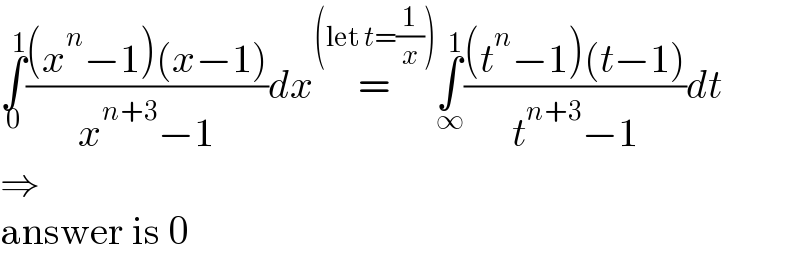
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\left({x}^{{n}} −\mathrm{1}\right)\left({x}−\mathrm{1}\right)}{{x}^{{n}+\mathrm{3}} −\mathrm{1}}{dx}\overset{\left(\mathrm{let}\:{t}=\frac{\mathrm{1}}{{x}}\right)} {=}\underset{\infty} {\overset{\mathrm{1}} {\int}}\frac{\left({t}^{{n}} −\mathrm{1}\right)\left({t}−\mathrm{1}\right)}{{t}^{{n}+\mathrm{3}} −\mathrm{1}}{dt} \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is}\:\mathrm{0} \\ $$
