Question Number 175608 by ajfour last updated on 03/Sep/22
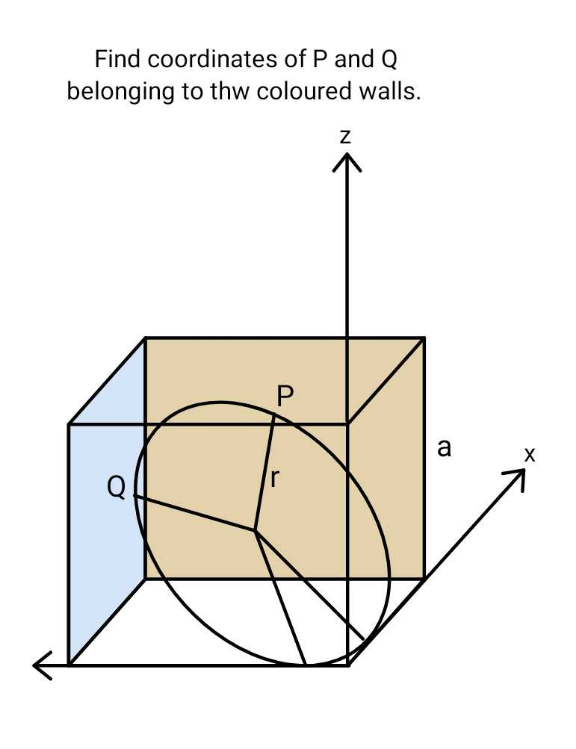
Commented by ajfour last updated on 04/Sep/22

$${yes}\:{sir}. \\ $$
Commented by mr W last updated on 04/Sep/22
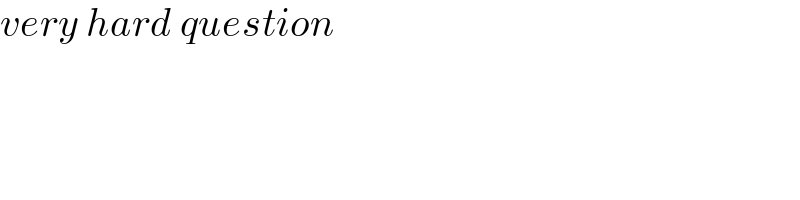
$${very}\:{hard}\:{question} \\ $$
Commented by mr W last updated on 04/Sep/22
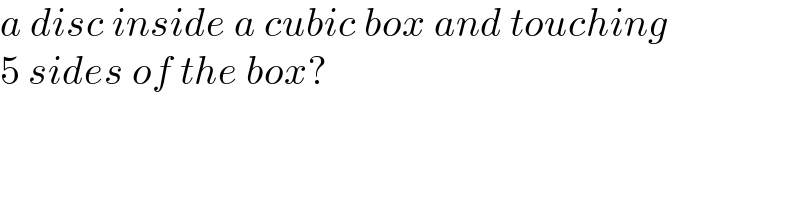
$${a}\:{disc}\:{inside}\:{a}\:{cubic}\:{box}\:{and}\:{touching} \\ $$$$\mathrm{5}\:{sides}\:{of}\:{the}\:{box}? \\ $$
Answered by mr W last updated on 06/Sep/22
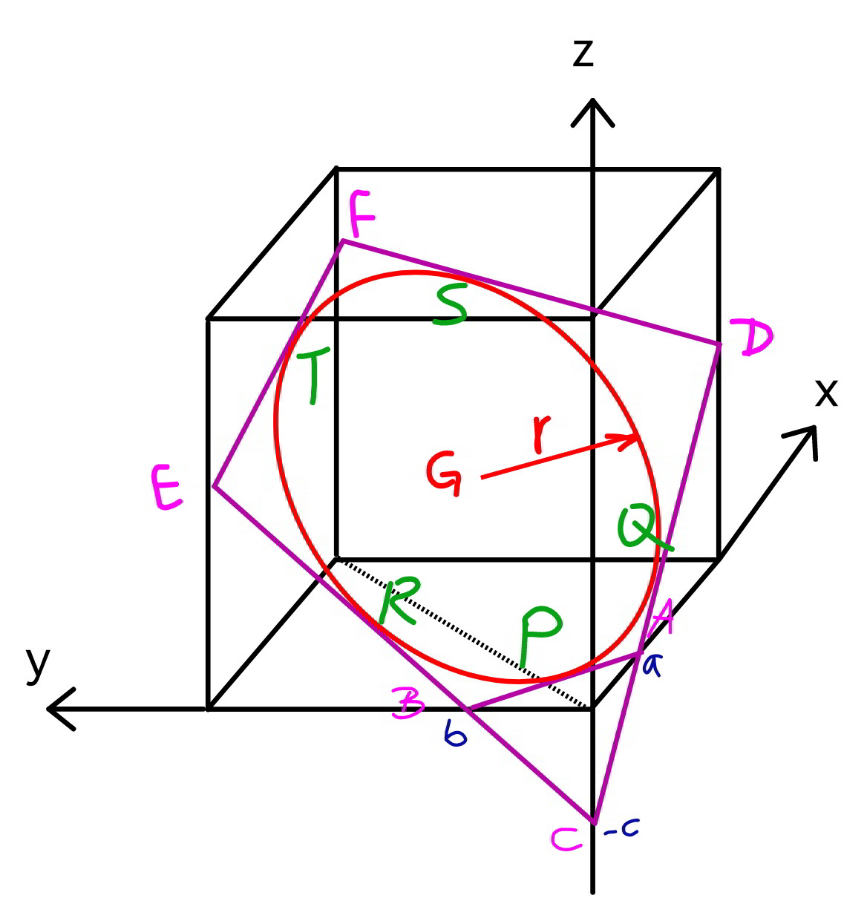
Commented by mr W last updated on 06/Sep/22
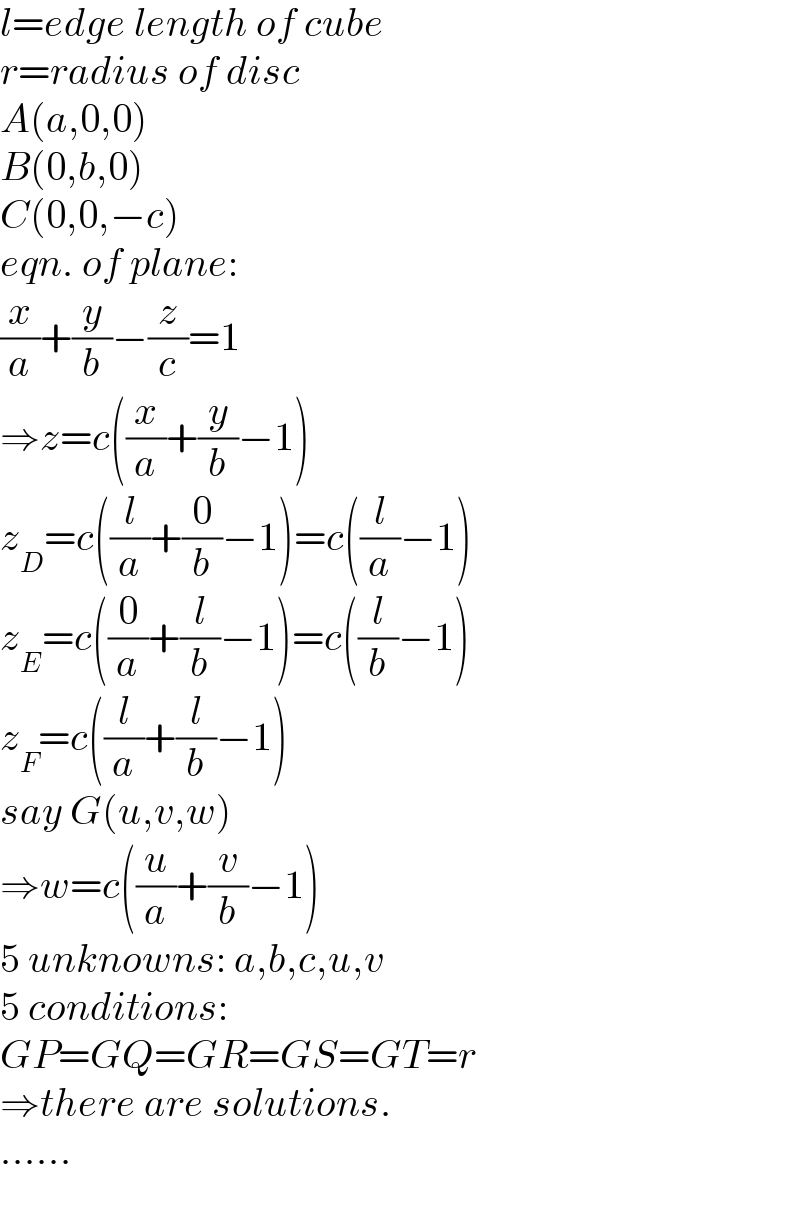
$${l}={edge}\:{length}\:{of}\:{cube} \\ $$$${r}={radius}\:{of}\:{disc} \\ $$$${A}\left({a},\mathrm{0},\mathrm{0}\right) \\ $$$${B}\left(\mathrm{0},{b},\mathrm{0}\right) \\ $$$${C}\left(\mathrm{0},\mathrm{0},−{c}\right) \\ $$$${eqn}.\:{of}\:{plane}: \\ $$$$\frac{{x}}{{a}}+\frac{{y}}{{b}}−\frac{{z}}{{c}}=\mathrm{1} \\ $$$$\Rightarrow{z}={c}\left(\frac{{x}}{{a}}+\frac{{y}}{{b}}−\mathrm{1}\right) \\ $$$${z}_{{D}} ={c}\left(\frac{{l}}{{a}}+\frac{\mathrm{0}}{{b}}−\mathrm{1}\right)={c}\left(\frac{{l}}{{a}}−\mathrm{1}\right) \\ $$$${z}_{{E}} ={c}\left(\frac{\mathrm{0}}{{a}}+\frac{{l}}{{b}}−\mathrm{1}\right)={c}\left(\frac{{l}}{{b}}−\mathrm{1}\right) \\ $$$${z}_{{F}} ={c}\left(\frac{{l}}{{a}}+\frac{{l}}{{b}}−\mathrm{1}\right) \\ $$$${say}\:{G}\left({u},{v},{w}\right) \\ $$$$\Rightarrow{w}={c}\left(\frac{{u}}{{a}}+\frac{{v}}{{b}}−\mathrm{1}\right) \\ $$$$\mathrm{5}\:{unknowns}:\:{a},{b},{c},{u},{v} \\ $$$$\mathrm{5}\:{conditions}:\: \\ $$$${GP}={GQ}={GR}={GS}={GT}={r} \\ $$$$\Rightarrow{there}\:{are}\:{solutions}. \\ $$$$…… \\ $$
Commented by ajfour last updated on 06/Sep/22

$${In}\:{question},\:{bottom}\:{of}\:{ring}\:{touches} \\ $$$${at}\:{points}\:{one}\:{along}\:{x}\:{and}\:{one} \\ $$$${along}\:{y},\:{shouldnt}\:{be}\:{as}\:{tough} \\ $$$${then},\:{sir}.. \\ $$
Commented by mr W last updated on 06/Sep/22

$${that}\:{makes}\:{the}\:{thing}\:{a}\:{little}\:{bit} \\ $$$${easier}.\:{but}\:{then}\:{the}\:{ring}\:{is}\:{no} \\ $$$${longer}\:{completely}\:{inside}\:{the}\:{box} \\ $$$${and}\:{there}\:{are}\:{no}\:{unique}\:{solutions}. \\ $$
Commented by mr W last updated on 06/Sep/22
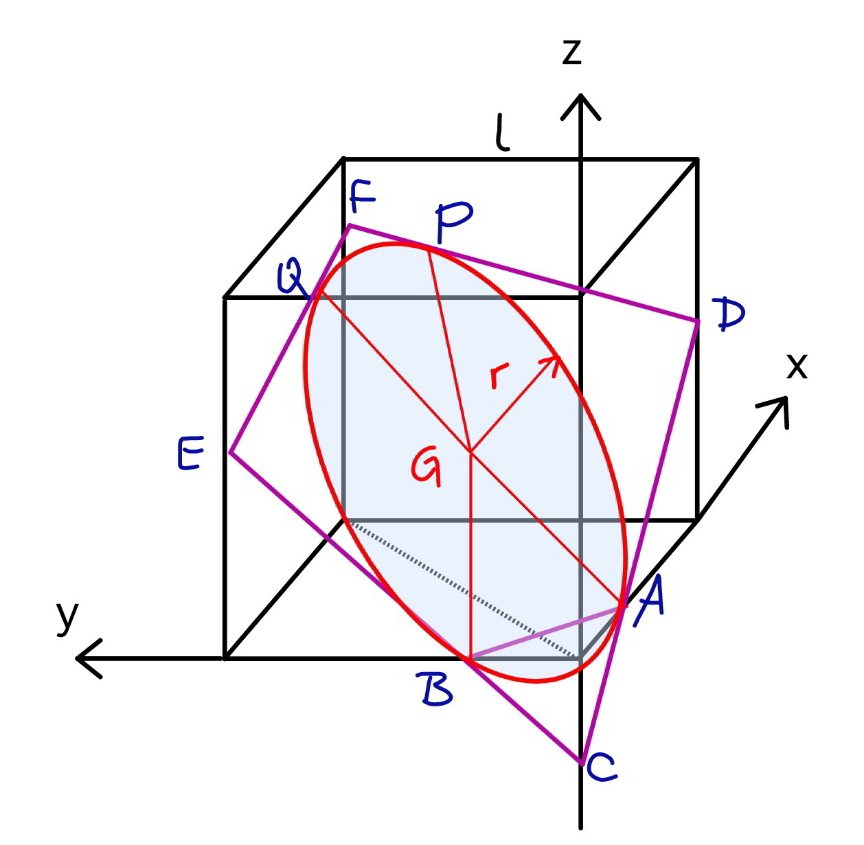
Commented by ajfour last updated on 07/Sep/22
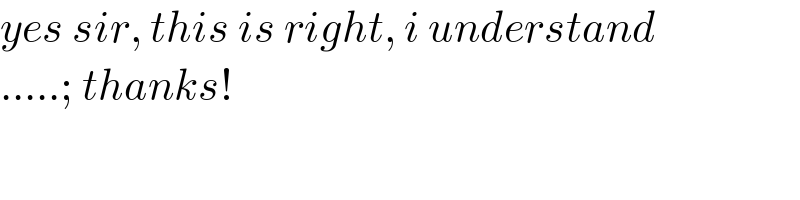
$${yes}\:{sir},\:{this}\:{is}\:{right},\:{i}\:{understand} \\ $$$$…..;\:{thanks}! \\ $$
Commented by Tawa11 last updated on 15/Sep/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
