Question-175750

Question Number 175750 by Shrinava last updated on 06/Sep/22

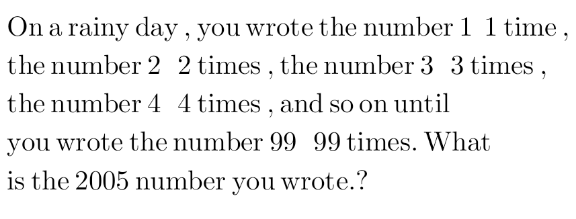
Answered by mr W last updated on 06/Sep/22

1 time 1 2 times 2 3 times 3 ... n−1 times n−1 n times n number of numbers before the first number n is 1+2+3+...+(n−1), so the first number n is the x^(th) number. x=1+2+3+...+(n−1)+1=((n(n−1))/2)+1 ((n(n−1))/2)+1≥2005 n(n−1)≥4008 ⇒n≥64 i.e. the 2005^(th) number is 64

$$\mathrm{1}\:{time}\:\mathrm{1} \\ $$$$\mathrm{2}\:{times}\:\mathrm{2} \\ $$$$\mathrm{3}\:{times}\:\mathrm{3} \\ $$$$… \\ $$$${n}−\mathrm{1}\:{times}\:{n}−\mathrm{1} \\ $$$${n}\:{times}\:{n} \\ $$$${number}\:{of}\:{numbers}\:{before}\:{the}\:{first} \\ $$$${number}\:{n}\:{is}\:\mathrm{1}+\mathrm{2}+\mathrm{3}+…+\left({n}−\mathrm{1}\right),\:{so} \\ $$$${the}\:{first}\:{number}\:{n}\:{is}\:{the}\:{x}^{{th}} \:{number}.\: \\ $$$${x}=\mathrm{1}+\mathrm{2}+\mathrm{3}+…+\left({n}−\mathrm{1}\right)+\mathrm{1}=\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}+\mathrm{1} \\ $$$$\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}+\mathrm{1}\geqslant\mathrm{2005} \\ $$$${n}\left({n}−\mathrm{1}\right)\geqslant\mathrm{4008}\:\Rightarrow{n}\geqslant\mathrm{64} \\ $$$${i}.{e}.\:{the}\:\mathrm{2005}^{{th}} \:{number}\:{is}\:\mathrm{64} \\ $$

Commented by Shrinava last updated on 06/Sep/22

thank you so much dear professor but how did it happen without mentioning +1

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{dear}\:\mathrm{professor} \\ $$$$\mathrm{but}\:\mathrm{how}\:\mathrm{did}\:\mathrm{it}\:\mathrm{happen}\:\mathrm{without} \\ $$$$\mathrm{mentioning}\:+\mathrm{1} \\ $$

Commented by mr W last updated on 06/Sep/22

the first number n is the [1+2+3+...+(n−1)+1]^(th) number.

$${the}\:{first}\:{number}\:{n}\:{is}\:{the} \\ $$$$\left[\mathrm{1}+\mathrm{2}+\mathrm{3}+…+\left({n}−\mathrm{1}\right)+\mathrm{1}\right]^{{th}} \:{number}. \\ $$

Commented by Shrinava last updated on 06/Sep/22

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor} \\ $$

Commented by Tawa11 last updated on 15/Sep/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply