Question Number 175756 by mnjuly1970 last updated on 06/Sep/22
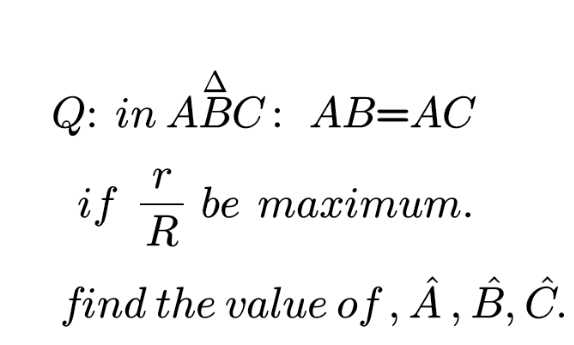
Commented by mr W last updated on 06/Sep/22

$${i}\:{think}\:{for}\:{any}\:{type}\:{of}\:{triangle}, \\ $$$$\frac{{r}}{{R}}\:{is}\:{maximum}\:{when}\:{A}={B}={C}=\mathrm{60}°. \\ $$
Answered by mr W last updated on 06/Sep/22
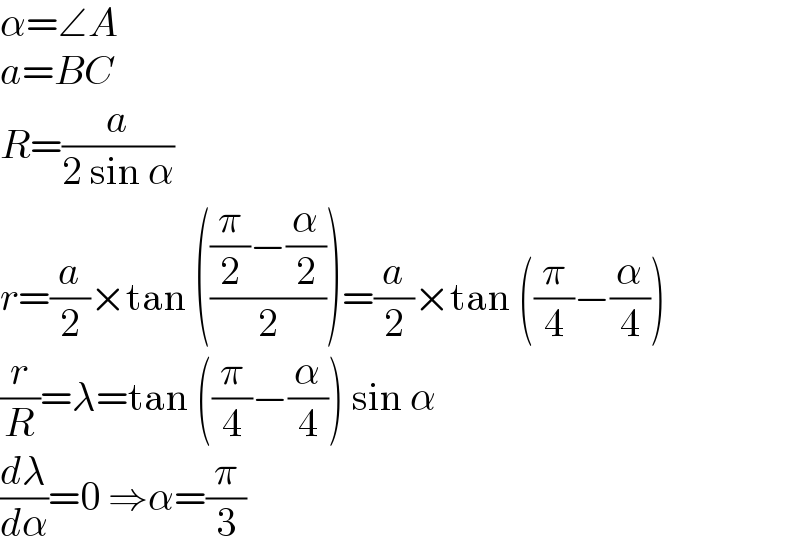
$$\alpha=\angle{A} \\ $$$${a}={BC} \\ $$$${R}=\frac{{a}}{\mathrm{2}\:\mathrm{sin}\:\alpha} \\ $$$${r}=\frac{{a}}{\mathrm{2}}×\mathrm{tan}\:\left(\frac{\frac{\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}}}{\mathrm{2}}\right)=\frac{{a}}{\mathrm{2}}×\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{4}}\right) \\ $$$$\frac{{r}}{{R}}=\lambda=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{4}}\right)\:\mathrm{sin}\:\alpha \\ $$$$\frac{{d}\lambda}{{d}\alpha}=\mathrm{0}\:\Rightarrow\alpha=\frac{\pi}{\mathrm{3}} \\ $$
Answered by behi834171 last updated on 06/Sep/22

$${max}\:{of}:\:\frac{{R}}{\boldsymbol{{r}}}=\mathrm{2}\Rightarrow{according}\:{to}\:{euler}'{s}\:{rule} \\ $$$$\boldsymbol{{d}}^{\mathrm{2}} =\boldsymbol{{R}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{R}}.\boldsymbol{{r}}\:\:\:\:\overset{\boldsymbol{{R}}=\mathrm{2}\boldsymbol{{r}}} {\Rightarrow}\:\:\:\boldsymbol{{d}}=\mathrm{0} \\ $$$$\boldsymbol{{d}},{is}\:\boldsymbol{{distance}}\:\boldsymbol{{among}}\:\boldsymbol{{centers}}\:\boldsymbol{{of}}\: \\ $$$$\boldsymbol{{incircle}}\:\boldsymbol{{and}}\:\boldsymbol{{outcircle}}. \\ $$$$\boldsymbol{{only}}\:\boldsymbol{{in}}\:\boldsymbol{{equilateral}}\:\boldsymbol{{triangle}}\:\boldsymbol{{d}}=\mathrm{0} \\ $$$$\boldsymbol{{so}}:\:\:\angle{A}=\angle{B}=\angle{C}=\mathrm{60}^{\bullet} \:\:\:\:.\blacksquare \\ $$
